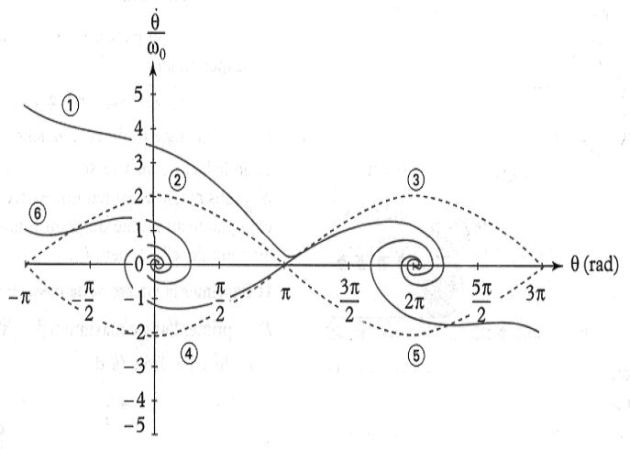
Portraits de phase
Définition : Notion d'espace des phases
Cet espace est le produit de l'espace ordinaire par l'espace des vitesses.
En d'autres termes, un point matériel M est repéré dans cet espace par les coordonnées (x,y,z) de son vecteur position ainsi que par celles de son vecteur vitesse, notées (vx,vy,vz).
On se limite aux cas où un point matériel M est animé, dans l'espace ordinaire, d'un mouvement à une dimension, le long de l'axe (Ox).
Dans l'espace des phases, le point représentatif de l'état de M se déplace alors dans une région à deux dimensions.
Ce point, de coordonnées (x,v), décrit lors du mouvement de M une courbe appelée "courbe des phases".
Cette "trajectoire" de M dans l'espace des phases a pour origine le point M0(x0,v0) correspondant à l'état initial de M.
La position du point matériel est complètement déterminée par la donnée des conditions initiales et par la connaissance des équations du mouvement.
Comme l'évolution de la particule est univoque, deux trajectoires dans l'espace des phases ne peuvent pas se croiser.
Si cela était possible, en prenant ce point d'intersection comme conditions initiales, on pourrait obtenir deux solutions distinctes des équations du mouvement, ce qui est interdit pour des raisons mathématiques.
Exemple : Approche du portrait de phase
On considère un pendule simple de longueur
que l'on écarte sans vitesse initiale de l'angle
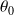par rapport à la verticale descendante.
Le pendule est soumis à des frottements fluides et son équation différentielle devient :
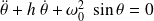
Son portrait de phase est donné sur la figure suivante, avec :
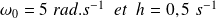
A quoi voit-on qu'il y a des frottements ?
Indiquer les positions d'équilibre stables et instables.
Commenter l'allure des différentes courbes.
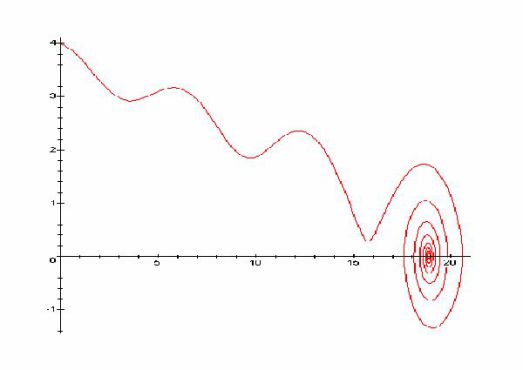
Comment interpréter la figure précédente ?
