Forces d'inertie d'entraînement et de Coriolis
Fondamental : Utilité mathématique des forces d'inertie
(R) est un référentiel galiléen et (R') un référentiel en mouvement quelconque par rapport à (R).
Un point matériel M (m) est soumis à des forces (« réelles ») dont la résultante est nommée
.
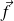On note
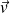et
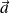la vitesse et l'accélération de M dans (R).
On note
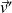et
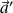la vitesse et l'accélération de M dans (R').
On rappelle que, dans le cas général :
Le PFD appliqué dans le référentiel galiléen (R) donne :
En utilisant la composition des accélérations :
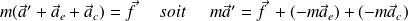
On pose :
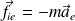: force d'inertie d'entraînement
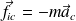: force d'inertie de Coriolis
Alors :
On peut ainsi appliquer un « pseudo » PFD dans un référentiel non galiléen, à condition de rajouter aux forces « réelles » les forces d'inertie d'entraînement et de Coriolis.
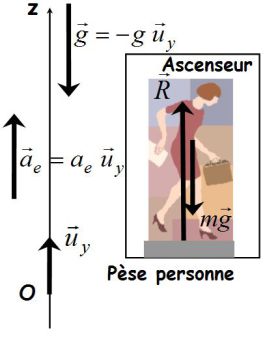
Exemple : Ascenseur et poids apparent
Dans le cas ici d'un mouvement de translation du référentiel (R') par rapport au référentiel (R), il n'y a pas de force de Coriolis.
L'équilibre « relatif », dans le référentiel de l'ascenseur, s'écrit :
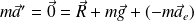
Soit, en introduisant la notion de « poids apparent », Papp :
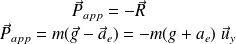
Remarque : g est en valeur absolue (g > 0) alors que ae est en valeur algébrique (> ou < 0).
Quand l'ascenseur démarre du rez de chaussée vers le 6ème étage par exemple, ae est positive et donc le poids apparent est supérieur au poids réel, ce qui est conforme à ce que l'on ressent effectivement dans un ascenseur.
On peut remarquer que le poids apparent s'annule quand l'ascenseur tombe en chute libre !
Remarque :
Si le référentiel (R') est en mouvement de translation rectiligne uniforme par rapport à (R), l'accélération d'entraînement est nulle.
Alors :
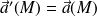
Et le PFD dans (R') s'écrit :
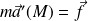
Le PFD est donc valable dans le référentiel (R').
On montre ainsi qu'un référentiel en translation rectiligne uniforme par rapport à un référentiel galiléen est lui-même galiléen.
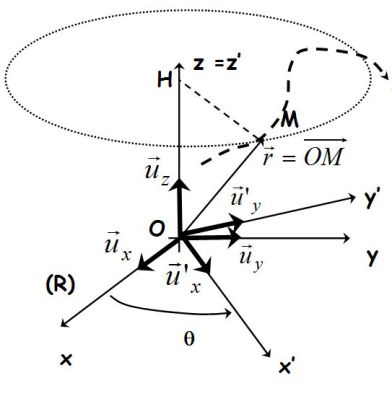
Exemple : La force d'inertie d'entraînement (force centrifuge)
Le mouvement d'entraînement de (R') par rapport à (R) est une rotation autour d'un axe fixe.
On suppose la vitesse angulaire de rotation
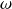constante.
La force d'inertie vaut alors :
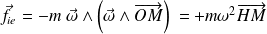
C'est la force centrifuge bien connue !
Exemple : La force d'inertie de Coriolis
Si
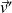désigne la vitesse du point matériel dans le référentiel (R'), la force de Coriolis s'écrit :
Des effets de la force de Coriolis en mécanique terrestre sont donnés dans le rappel de cours sur les référentiels non galiléens.
