Quelques applications classiques
Fondamental : Oscillateur harmonique amorti par frottement fluide (régime libre)
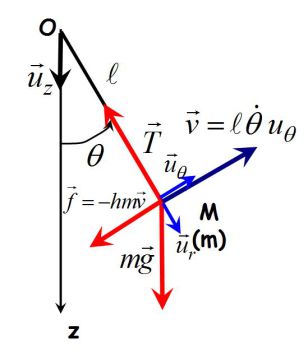
Un oscillateur harmonique amorti par frottement fluide obéit à l'équation différentielle suivante (cas à une dimension) :
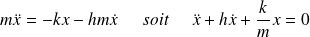
On pose :

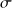 est le facteur d'amortissement de l'oscillateur et Q le facteur de qualité.
est le facteur d'amortissement de l'oscillateur et Q le facteur de qualité.
Alors :

On recherche des solutions de la forme exp(rt), avec r appartenant a priori au corps des complexes.
On aboutit au polynôme caractéristique :
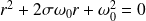
dont le discriminant est :
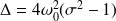
Différents régimes sont observés, selon les valeurs prises par
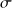 (ou
(ou
 ) :
) :
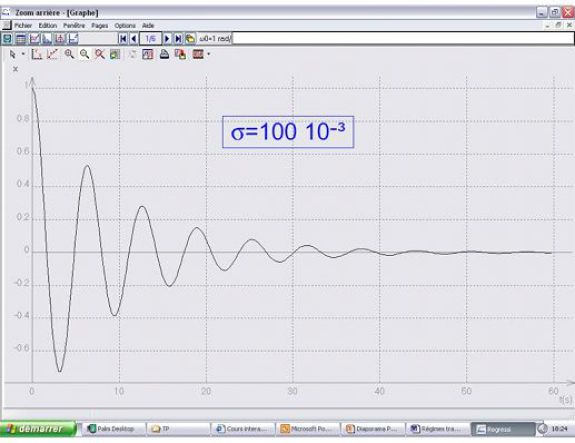
régime pseudo-périodique : alors
Dans le cas où
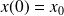 et la vitesse initiale nulle :
et la vitesse initiale nulle : 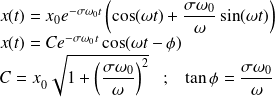
Avec :
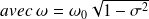
la pseudo-pulsation.
On peut noter que le facteur de qualité
 donne l'ordre de grandeur du nombre de pseudo-oscillations visibles expérimentalement.
donne l'ordre de grandeur du nombre de pseudo-oscillations visibles expérimentalement.
régime apériodique : alors
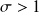
Dans le cas où
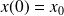 et la vitesse initiale nulle :
et la vitesse initiale nulle : 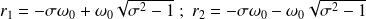

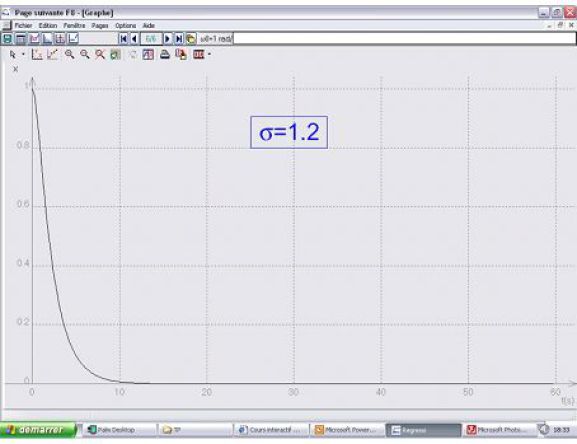
régime apériodique critique : alors
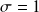
Dans le cas où
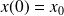 et la vitesse initiale nulle :
et la vitesse initiale nulle : 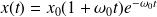

Régimes pseudo-périodique et apériodique
Une vidéo sur les oscillations d'un flotteur
Fondamental : Le pendule simple
En présence d'une force de frottement fluide de la forme :
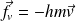
Le PFD projeté sur le vecteur
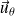 donne : (on peut aussi utiliser le théorème du moment cinétique)
donne : (on peut aussi utiliser le théorème du moment cinétique)
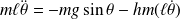
Soit :
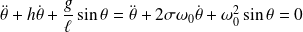
Si l'angle
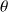 reste « petit », alors on retrouve l'équation habituelle :
reste « petit », alors on retrouve l'équation habituelle :
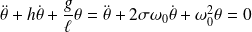
Exemple : Oscillateurs mécaniques en régime sinusoïdal forcé
Une résonance mécanique impressionnante : la vidéo du pont de Tacoma qui rentre en résonance
Exemple : Une animation sur la résonance (University of Colorado Boulder)
Observer la résonance dans une collection d'oscillateurs harmoniques amortis et pilotés.
Faire varier la fréquence et l'amplitude du pilotage, la constante d'amortissement, et la masse et la constante du ressort de chaque résonateur.
Noter les transitoires de longue durée lorsque l'amortissement est faible, et observer le changement de phase pour les résonateurs dessus et en dessous de résonance.
Fondamental : Oscillateurs mécaniques en régime sinusoïdal forcé
Intérêt de l'étude :
L'analyse harmonique (ou fréquentielle) d'un système est son étude au moyen de sa réponse harmonique s(t), c'est-à-dire de sa réponse en régime permanent sinusoïdal lorsqu'il est soumis à une entrée sinusoïdale e(t) dont on fait varier la pulsation ω.
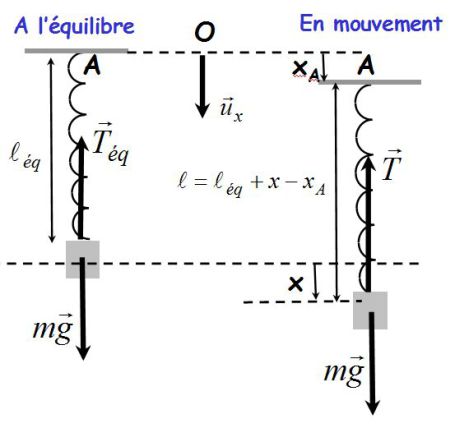
Modèle choisi : oscillateur mécanique vertical à point d'attache mobile
Le point d'attache du ressort est mobile en A.
Dans le référentiel galiléen du sol :

En utilisant la condition d'équilibre :
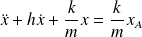
Soit, avec les notations habituelles :
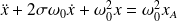
Dans la suite, on choisit :
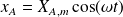
Cette équation est formellement identique à celle vérifiée par la tension aux bornes d'un condensateur dans un circuit série (RLC) alimenté par un GBF (voir cours d'électricité) :
Si on note
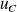 la tension aux bornes du condensateur : (
la tension aux bornes du condensateur : (
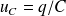 )
)
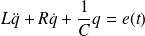
Soit :
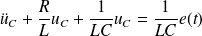
Méthode de résolution par les nombres complexes (comme en électricité) :
On pose :
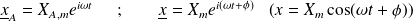
Alors :
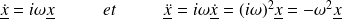
Réponse en amplitude
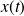 :
:
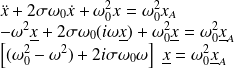
Soit :
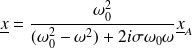
Ou encore :
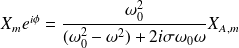
L'amplitude maximale s'obtient en prenant le module de l'expression précédente :
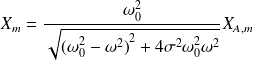
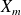 est maximale pour une pulsation qui vaut (et qui existe si
est maximale pour une pulsation qui vaut (et qui existe si
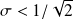 ) :
) :
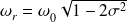
Et l'amplitude maximale à la « résonance d'amplitude » est :
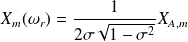
Les formules précédentes deviennent, en utilisant le facteur de qualité Q à la place du coefficient d'amortissement
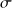 : (
: (
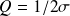 ) :
) :

Et :
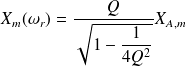
Remarque :
Pour de faibles amortissements (
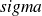 "faible" et
"faible" et
 "grand"), alors :
"grand"), alors :

Ainsi, si
 , l'amplitude lors de la résonance vaut 10 fois celle de l'excitation : la résonance est dite «aiguë» et peut causer la destruction du système oscillant.
, l'amplitude lors de la résonance vaut 10 fois celle de l'excitation : la résonance est dite «aiguë» et peut causer la destruction du système oscillant.
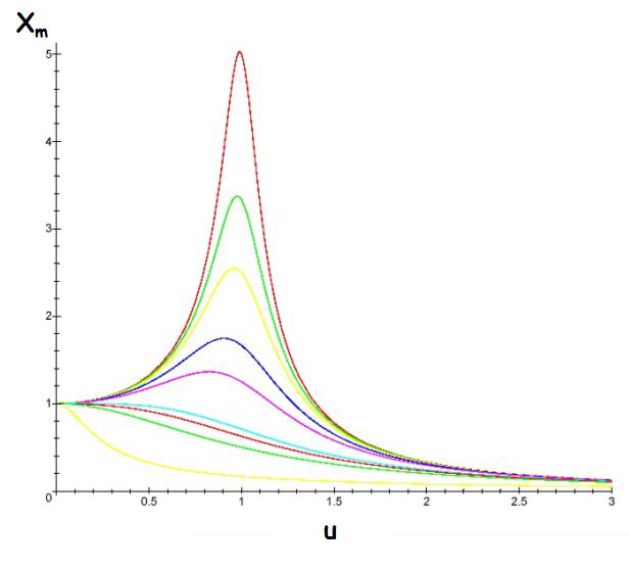
La figure précédente donne l'allure de
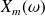 pour différentes valeurs du facteur de qualité
pour différentes valeurs du facteur de qualité
 .
.
On a choisi
 et posé
et posé
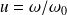 .
.
Plus Q est grand et plus la résonance est aigüe.
L'oscillateur constitue un filtre passe-bas, avec ou sans résonance.
Réponse en vitesse :
En notation réelle :
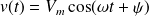
En notation complexe :
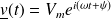
En remarquant que
 , il vient :
, il vient :
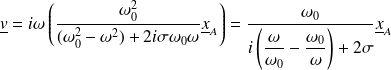
Ou encore :
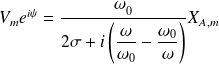
L'amplitude maximale de la vitesse
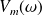 s'obtient à partir du module :
s'obtient à partir du module :
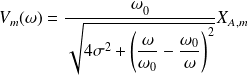
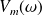 sera maximale (on parle alors de résonance de vitesse), si le dénominateur est minimal, c'est à dire pour une pulsation telle que :
sera maximale (on parle alors de résonance de vitesse), si le dénominateur est minimal, c'est à dire pour une pulsation telle que :
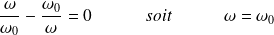
L'amplitude de la vitesse valant alors :
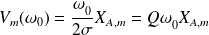
La figure précédente donne l'allure de
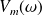 pour différentes valeurs du facteur de qualité
pour différentes valeurs du facteur de qualité
 .
.
On a choisi
 et posé
et posé
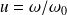 .
.
Plus Q est grand et plus la résonance est aigüe.
L'oscillateur constitue un filtre passe-bande.
Bande passante du filtre passe-bande :
C'est l'ensemble des pulsations ω pour lesquelles le gain en vitesse reste, par convention, supérieur au gain maximal (obtenu pour ω0) divisé par
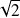 .
.
La largeur de la bande passante vaut :
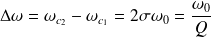
Elle est d'autant plus faible (résonance aiguë) que l'amortissement est faible (et le facteur de qualité grand).
Simulation : Animations JAVA de JJ.Rousseau (Université du Mans)
Suspension d'un véhicule : cliquer ICI
Oscillations amorties (frottements visqueux ou solide) : cliquer ICI
Molécule biatomique (modèle harmonique) : cliquer ICI
Potentiel de Morse : cliquer ICI
Potentiel de Lennard-Jones : cliquer ICI
Satellite géostationnaire : cliquer ICI
Satellite artificiel : cliquer ICI
Trajectoires célestes possibles : cliquer ICI
Les satellites GPS : cliquer ICI