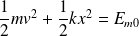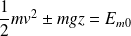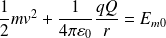Les principes de la mécanique newtonienne
Fondamental : Le principe d'inertie
« Tout corps persévère dans l'état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n'agisse sur lui, et ne le contraigne à changer d'état ».
Ce principe n'est valable que dans les référentiels galiléens.
Une autre version du principe d'inertie, couramment admise :
Il existe une classe de référentiels, appelés galiléens, par rapport auxquels un objet ponctuel isolé est soit immobile soit en mouvement rectiligne uniforme.
Définition : Référentiels galiléens couramment utilisés :
On appelle référentiel galiléen un référentiel dans lequel le principe d'inertie est vérifié.
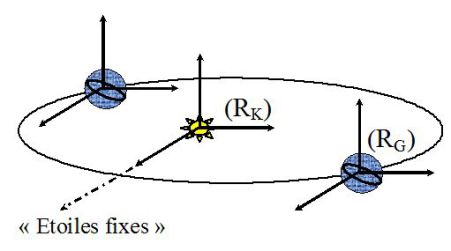
le référentiel héliocentrique (de Kepler) d'origine le centre du soleil et dont les trois axes sont dirigés vers des étoiles ‘fixes'.
le référentiel géocentrique d'origine le centre de la terre et dont les axes sont parallèles aux précédents.
le référentiel terrestre (du laboratoire), pour toutes les applications courantes.
Tous les référentiels galiléens sont en translations uniformes les uns par rapport aux autres.
Fondamental : Le principe fondamental de la dynamique (PFD)
Le PFD permet d'évaluer les variations de la quantité de mouvement
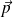 dues aux forces (de résultante
dues aux forces (de résultante
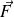 ) exercées sur un objet ponctuel (de masse
) exercées sur un objet ponctuel (de masse
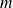 ).
).
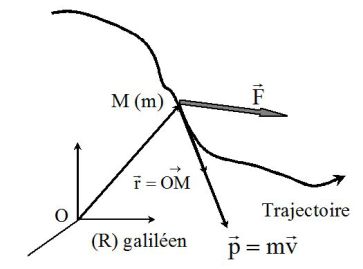
Dans un référentiel galiléen, le PFD s'écrit :
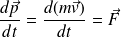
Fondamental : Le principe des actions réciproques
Si un corps A exerce une force
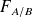 sur un corps B, alors ce corps B exerce sur A la force opposée :
sur un corps B, alors ce corps B exerce sur A la force opposée :
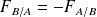
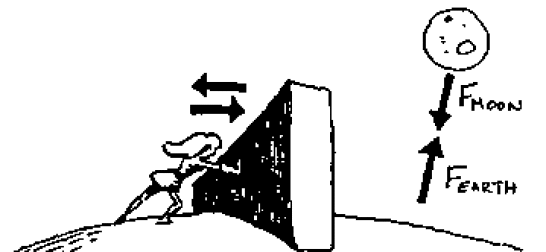
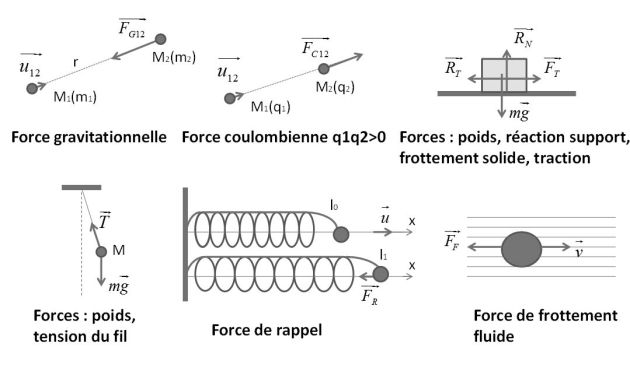
Exemple : Des exemples de forces
Une animation JAVA de JJ.Rousseau (Université du Mans) sur l'expérience de Cavendish :
Expérience de Cavendish : cliquer ICI
Fondamental : Le théorème du centre d'inertie
On se place dans un référentiel galiléen et on considère un ensemble de n points matériels, notés Mi, de masse mi.
Le mouvement du centre d'inertie d'un système de points matériels est celui d'un point qui aurait la masse totale du système et auquel serait appliquée la somme des forces extérieures au système (la somme des forces intérieures est nulle, en vertu du principe des actions réciproques) :
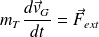
où
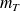 est la masse totale du système.
est la masse totale du système.
On rappelle que le centre d'inertie G d'un système de points matériels Mi de masse mi est le barycentre des points Mi affectés des coefficients mi, soit :

Si O est l'origine du référentiel d'étude, alors :
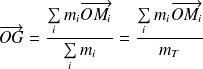
Fondamental : Théorème du moment cinétique
Soit O un point fixe d'un référentiel galiléen.
Un point matériel, de vitesse
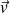 dans ce référentiel, est soumis à une force
dans ce référentiel, est soumis à une force
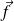 .
.
Soit
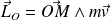 le moment cinétique du point M par rapport à O.
le moment cinétique du point M par rapport à O.
Le théorème du moment cinétique s'écrit :
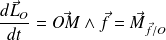
où
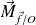 représente le moment de la force
représente le moment de la force
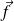 par rapport à O.
par rapport à O.
Méthode : Interprétation du moment des forces par rapport à O
La norme du moment de la force
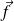 par rapport à O vaut :
par rapport à O vaut :

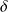 est appelé « bras de levier » de la force
est appelé « bras de levier » de la force
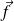 .
.
C'est la distance entre la droite d'action de la force et le point O.
Fondamental : Théorème de l'énergie cinétique
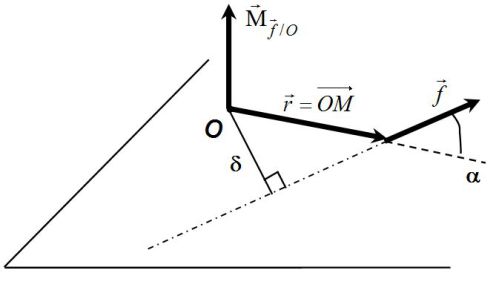
Le PFD appliqué au point matériel dans le référentiel (R) supposé galiléen donne :
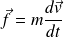
On multiplie scalairement cette équation par le vecteur vitesse :
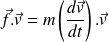
Or :
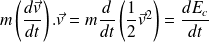
Par conséquent :
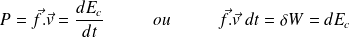
Deux énoncés :
La variation d'énergie cinétique d'un point matériel est égale à la somme des travaux des forces qui lui sont appliquées (théorème de l'énergie cinétique)
La puissance des forces est égale à la dérivée de l'énergie cinétique (théorème de la puissance cinétique)
Fondamental : Énergie mécanique et intégrale première du mouvement
Force | Intégrale première du mouvement |
Tension d'un ressort |
|
Champ de pesanteur |
|
Champ gravitationnel (newtonien) |
|
Champ électrostatique (coulombien) |
|
Exemple : vitesse de libération (interaction gravitationnelle)
Quelle vitesse initiale minimale
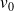 faut-il communiquer à un point matériel situé à la surface de la Terre pour qu'il échappe à l'attraction gravitationnelle terrestre ?
faut-il communiquer à un point matériel situé à la surface de la Terre pour qu'il échappe à l'attraction gravitationnelle terrestre ?
On veut que le point matériel arrive à l'infini (où l'énergie potentielle est nulle) avec une vitesse nulle (c'est la condition pour avoir
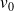 minimale). Par conséquent :
minimale). Par conséquent :
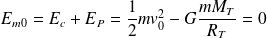
Soit :
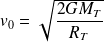
Avec :

On obtient :
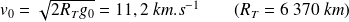
Simulation : Animations JAVA de JJ.Rousseau (Université du Mans)
Escarpolette (ou comment faire de la balançoire ?) : cliquer ICI