Charges aux sommets d'un carré
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Quatre charges identiques q sont placées aux quatre sommets d'un carré de côté a
.
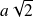Elles sont fixes.
Question
Déterminer le mouvement d'une charge q' de masse m au voisinage immédiat du centre du carré (q et q' sont de même signe).
On se placera en coordonnées cartésiennes et on fera un développement de Taylor du potentiel électrostatique, en tenant compte des symétries du problème et en considérant des cas particuliers.
Pourquoi peut-on écrire le potentiel en un point M sous la forme ?
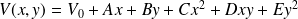
Simplifier cette expression en utilisant les symétries.
Le potentiel électrostatique en un point M proche de l'origine peut s'écrire sous la forme d'un développement de Taylor au 2nd ordre :
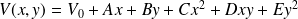
V0 désigne le potentiel à l'origine :
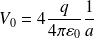
Par symétrie :
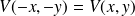donc A = B = 0.
De même :
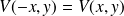donc D = 0.
Enfin :
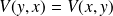donne C = E.
Finalement, avec r = OM :
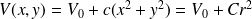
Pour déterminer C, on considère que le point M a pour coordonnées M (x,0). Alors :
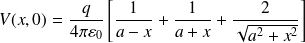
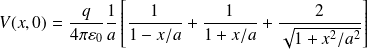
En faisant un développement limité au 2nd ordre en x / a :
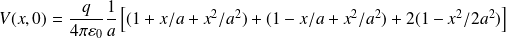
Soit :
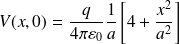
Par identification, on déduit :
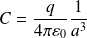
Le potentiel s'écrit donc sous la forme :
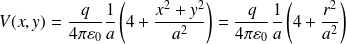
La force électrique subie par la charge q' est ensuite :
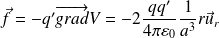
C'est une force de rappel.
Le PFD appliqué à la charge q' donne :
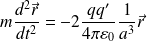
Soit :
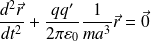
Avec :
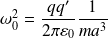
La solution de cette équation différentielle est :
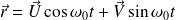
La trajectoire est, dans le cas général, une ellipse.
Simulation : Animation JAVA de JJ.Rousseau (Université du Mans)
Charges ponctuelles aux sommets d'un carré : cliquer ICI
