Vitesse de propagation de l'énergie
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Soit un champ électrique qui a la structure d'une onde plane progressive harmonique, d’amplitude E0, de pulsation ω, de vecteur d'onde k, se propageant selon Oz et polarisé selon Ox.
Question
Écrire l'expression du champ électrique
.
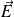En notation complexe :
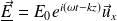
Question
Calculer la valeur moyenne de la densité volumique d'énergie électromagnétique en un point de l'espace.
Le champ magnétique se calcule à l'aide de la relation de structure :
Soit :
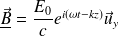
La valeur moyenne de la densité volumique d'énergie électromagnétique est alors :
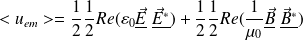
Soit, avec
:
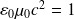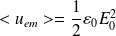
Question
Calculer la valeur moyenne du vecteur de Poynting.
La valeur moyenne du vecteur de Poynting est :
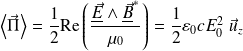
Question
Calculer la valeur moyenne de l'énergie
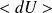sur un volume de surface dS = dxdy et d'épaisseur dz.
La valeur moyenne de l'énergie dans le volume est :
Question
Calculer le flux d'énergie
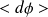à travers cette surface dS durant un intervalle de temps dt.
Le flux d'énergie
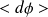à travers cette surface dS durant un intervalle de temps dt est relié au flux du vecteur de Poynting, qui est une puissance :
Question
En déduire la valeur de la vitesse de propagation de l'énergie électromagnétique. Commentaire.
Si
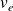désigne la vitesse de propagation de l'énergie, alors :
En égalant les deux énergies calculées aux questions précédentes :
Il reste :
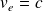
Ainsi, dans le vide (milieu non dispersif), la vitesse de propagation est celle de propagation de l'onde, soit c.
Les vitesses de phase et de groupe (correspondant souvent à la vitesse de propagation de l'énergie) sont égales.
