Étude de la forme d'un miroir métallique liquide
(10 minutes de préparation)
Cet exercice étudie le principe de fonctionnement et la mise en œuvre d'un miroir métallique liquide, utilisé dans des mesures astronomiques et atmosphériques.
Cet exercice propose de déterminer l'équation de la surface libre du miroir liquide mis en rotation.
Une cuve cylindrique de rayon R et de hauteur intérieure H, contient une hauteur h0 de liquide métallique incompressible de masse volumique
.
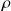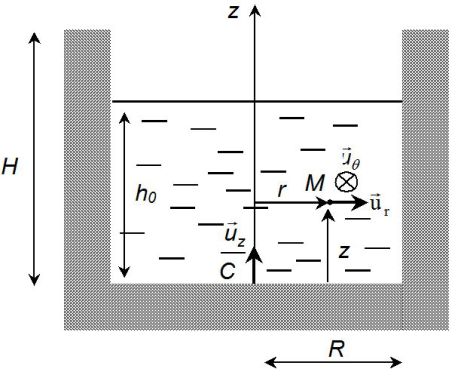
L'axe de symétrie (Cz) de la cuve est orienté suivant la verticale ascendante, le point origine C étant le centre du fond du récipient.
L'accélération de la pesanteur est notée
.
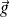Le référentiel d'étude (R) est celui du laboratoire supposé galiléen.
La cuve est ouverte à l'atmosphère à la pression P0.
La cuve est progressivement mise en rotation autour de (Cz) et, après une phase de démarrage suffisamment longue, la vitesse de rotation atteint une valeur constante
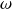, régulée avec précision.
Le liquide tourne également en bloc à la même vitesse angulaire autour de l'axe (Cz) et il est immobile par rapport au référentiel (R‘) lié à la cuve.
Question
On considère un volume
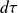de fluide centré sur un point M, de coordonnées cylindriques
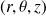dans le repère
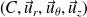du référentiel (R‘).
Écrire la condition d'équilibre relatif de ce volume élémentaire dans (R‘).
Dans le référentiel tournant (R') lié au fluide, le volume
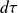de masse
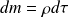est soumis aux trois forces :
Son poids
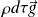
Les forces de pression
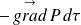
La force d'inertie d'entraînement centrifuge
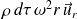
L'équilibre relatif du volume
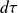donne :
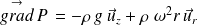
Question
En déduire que la surface libre du liquide a pour équation :
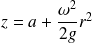
Où a est une constante. Quelle forme géométrique présente la surface libre ?
En coordonnées cylindriques, la pression P est a priori fonction de r,
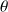et z et ainsi :
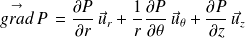
L'expression précédente projetée sur les vecteurs
,
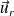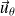et
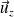donne alors :
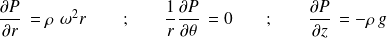
La pression ne dépend donc pas de l'angle
.
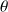Par intégration de la première équation :
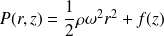
Où f(z) désigne une fonction de la seule variable z.
En dérivant partiellement cette dernière expression de P(r,z) puis en comparant avec la dernière équation :
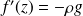
Soit :
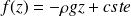
D'où finalement l'expression de la pression au sein du fluide :
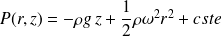
En tout point M de la surface libre du liquide, la pression est égale à la pression atmosphérique P0 ; par conséquent, les coordonnées de M vérifient l'équation :
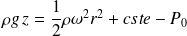
Finalement :
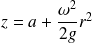
Où a désigne une nouvelle constante. La surface libre du liquide est une paraboloïde de révolution autour de l'axe (Cz).
La constante a peut être déterminée en écrivant la conservation du volume du liquide.
Simulation : Animation JAVA de JJ.Rousseau (Université du Mans)
Liquide en rotation uniforme : cliquer ICI
