Masse de l'atmosphère terrestre
(10 minutes de préparation)
On considère le modèle de l'atmosphère isotherme.
La pression à l'altitude z est donnée par : (isotherme à 0 °C)
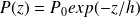
Avec
.
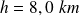Le rayon terrestre est
.
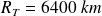Question
Estimer littéralement puis numériquement la masse matm de l'atmosphère terrestre en sachant que son épaisseur est grande devant h et petite devant le rayon terrestre
.
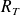Remarque :
Cet exercice peut être traité de manière plus "ludique", sous forme de problème "ouvert". Voir la rubrique "Résolution de problèmes ouverts".
Le modèle de l'atmosphère terrestre isotherme conduit à :
Avec :
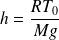
La masse volumique vaut, d'après la loi des GP :
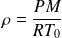
D'où une relation équivalente pour la masse volumique :
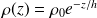
Avec :
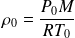
Soit H l'épaisseur de l'atmosphère (avec H >> h), alors la masse matm est donnée par :
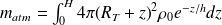
On suppose :
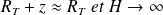
Donc :
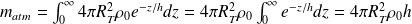
On obtient une masse équivalente à une atmosphère de masse volumique moyenne ρ0 et d'épaisseur h << RT.
On peut aussi remarquer, en utilisant les expressions de
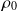et de
que :
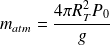
On voit alors que la force de pression sur la surface de la Terre (
) compense le poids
de la colonne d'air située au dessus.
