Pour tester sa connaissance du cours
Question
Donner l'expression volumique des forces de pression.
Donner l'expression volumique des forces de pesanteur (cas d'un champ uniforme).
L'expression volumique des forces de pression est :
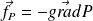
L'expression volumique des forces de pesanteur (cas d'un champ uniforme) est :
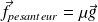
où
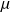 est la masse volumique du fluide.
est la masse volumique du fluide.
Question
Donner la relation fondamentale de la statique des fluides dans un référentiel galiléen.
Que devient-elle dans un référentiel non galiléen ?
La relation fondamentale de la statique des fluides dans un référentiel galiléen est :
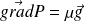
Dans un référentiel non galiléen, il faut prendre en compte la force d'inertie d'entraînement (en non celle de Coriolis qui est nulle puisque le fluide est au repos dans le référentiel non galiléen étudié).
Si on note
 l’accélération d'entraînement :
l’accélération d'entraînement : 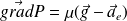
Question
Quelle est la valeur de la pression de l'eau dans la mer, à 10 m de profondeur ?
La pression est donnée par la relation (l'eau est un fluide incompressible) :

où
 est la profondeur.
est la profondeur.
Pour
 , on trouve
, on trouve
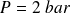 : la pression au sein de l'eau augmente de 1 bar tous les 10 m de profondeur.
: la pression au sein de l'eau augmente de 1 bar tous les 10 m de profondeur.
Question
Présenter le modèle de l'atmosphère isotherme. Quelle est l’expression de la pression en fonction de l'altitude ?
Que vaut la masse volumique en fonction de l'altitude ?
On suppose que l'atmosphère (considérée comme un gaz parfait) est à l'équilibre à température constante notée
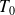 .
.La pression varie avec l'altitude
 selon la loi (appelée nivellement barométrique et en notant
selon la loi (appelée nivellement barométrique et en notant
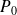 la pression au niveau du sol) :
la pression au niveau du sol) : 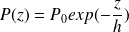
Où : (
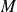 est la masse molaire de l'air)
est la masse molaire de l'air)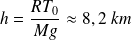
L'équation d'état d'un gaz parfait s'écrit :
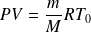
Par conséquent, la masse volumique vaut :

En notant
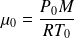 la masse volumique au niveau du sol (de l'ordre de
la masse volumique au niveau du sol (de l'ordre de
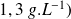 :
: 
Question
Donner le principe de quelques manomètres.
Les méthodes de mesures de pressions sont très nombreuses et diffèrent selon le domaine de pressions que l'on veut mesurer (qui peut s'étendre des basses pressions,
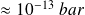 aux hautes pressions,
aux hautes pressions,
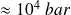 ).
).
La mesure des pressions moyennes (quelques dixièmes de bar à quelques bars) peut s'effectuer à partir de manomètres à dénivellation qui consistent à équilibrer une colonne de liquide (comme le baromètre de type Torricelli).
Les baromètres anéroïdes (c'est-à-dire sans liquide) permettent également la mesure de ces pressions.
La surpression (ou la dépression) à mesurer produit sur une membrane métallique élastique une déformation plus ou moins grande, que l'on amplifie par un système de leviers qui agit, par exemple, sur une aiguille indicatrice.
C'est un instrument à lecture directe, étalonné par comparaison avec un baromètre à mercure.
Les baromètres vendus dans le commerce sont très souvent basés sur ce principe.
On utilise aussi des capteurs piézo-électriques : un quartz piézo-électrique déformé par la pression appliquée produit un courant électrique dépendant de sa déformation.
Question
Énoncer le principe d'Archimède. Savez vous le démontrer "avec les mains" ?
Le principe d'Archimède s'énonce selon :
"Tout corps plongé dans un fluide subit de la part de celui-ci une force dirigée vers le haut et égale à l'opposé du poids du fluide déplacé" :
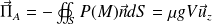
Où
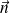 est le vecteur normal sortant,
est le vecteur normal sortant,
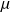 la masse volumique du fluide et
la masse volumique du fluide et
 le volume de fluide déplacé.
le volume de fluide déplacé.
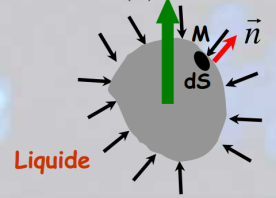
On isole par la pensée un volume d'eau identique au volume occupé par le solide immergé.
Le volume d'eau étant en équilibre, il est soumis à une force verticale dirigée vers le haut qui compense son poids, résultant des forces de pression du fluide environnant.
On place maintenant à la place le solide immergé ayant le même volume : la poussée du reste du fluide reste et égale donc (en norme) au poids du volume de fluide déplacé.
Question
Une sphère solide de rayon
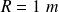 et de masse volumique
et de masse volumique
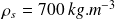 est entièrement immergée dans un réservoir rempli avec de l'eau.
est entièrement immergée dans un réservoir rempli avec de l'eau.
La sphère est attachée au fond du réservoir par une corde.
Quelle est la tension de la corde ?
Question
Quel est l'ordre de grandeur de la force de pression qui s'exerce sur une face d'une feuille de papier ?
Quelle est la masse dont le poids est équivalent à cette force ?
Si on prend une feuille de papier de format
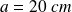 par
par
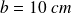 par exemple. La force de pression vaut : (
par exemple. La force de pression vaut : (
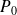 est la pression atmosphérique, égale à
est la pression atmosphérique, égale à
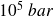 )
)
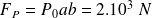
Soit le poids d'une masse d'environ
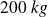 .
.
Heureusement, la pression atmosphérique s'exerce des deux côtés de la feuille !
Question
Deux demi-sphères sont collées l'une à l'autre. A l'intérieur, on a fait le vide (hémisphères de Magdebourg).
Le rayon des demi-sphères est
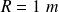 et la pression atmosphérique vaut
et la pression atmosphérique vaut
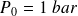 .
.
Estimer, sans gros calculs, la force minimale à exercer pour séparer les deux hémisphères.
La force exercée doit compenser la force due à la pression atmosphérique sur une demi-sphère, soit :
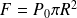
Globalement, tout se passe comme si la pression atmosphérique s'exerçait sur la surface du plan équatorial de la sphère.
Numériquement :
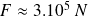
D'après vous, il a fallu combien de chevaux pour séparer les deux hémisphères ?






