Indépendance
Dans cette partie, on considère un espace probabilisé
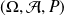 associé à une expérience aléatoire.
associé à une expérience aléatoire.
Définition :
Indépendance de deux événements
Deux événements
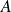 et
et
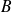 sont indépendants pour la probabilité
sont indépendants pour la probabilité
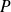 si :
si :
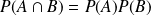 .
.
Conséquence : Les événements
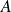 et
et
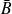 , les événements
, les événements
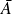 et
et
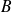 , les événements
, les événements
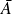 et
et
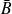 sont aussi indépendants.
sont aussi indépendants.
L'indépendance de
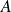 et
et
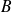 revient à dire qu'une information sur
revient à dire qu'une information sur
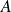 ou sur
ou sur
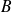 ne change pas la probabilité :
ne change pas la probabilité :
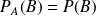 , et :
, et :
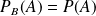 .
.
Attention :
Attention à ne pas confondre indépendance et incompatibilité.
Deux tribus
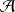 et
et
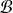 sont indépendantes si tout élément de
sont indépendantes si tout élément de
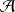 est indépendant de tout élément de
est indépendant de tout élément de
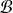 .
.
Si
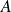 et
et
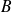 sont deux événements indépendants, les tribus engendrées par
sont deux événements indépendants, les tribus engendrées par
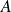 et
et
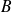 sont indépendantes.
sont indépendantes.
Définition :
Indépendance de plusieurs événements
Soit
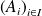 une famille d'événements avec
une famille d'événements avec
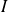 fini ou dénombrable.
fini ou dénombrable.
Les événements
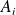 sont deux à deux indépendants si, pour tous
sont deux à deux indépendants si, pour tous
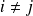 , les événements
, les événements
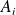 et
et
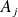 sont indépendants.
sont indépendants.Les événements
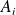 sont mutuellement indépendants si pour toute partie finie
sont mutuellement indépendants si pour toute partie finie
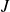 de
de
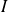 , on a :
, on a :
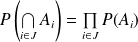 .
.
Dans les deux cas, les événements
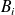 avec
avec
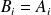 ou
ou
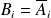 sont indépendants.
sont indépendants.
L'indépendance mutuelle entraîne l'indépendance deux à deux, mais la réciproque est fausse.





