Probabilité
Dans cette partie, on considère espace probabilisable
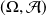associé à une expérience aléatoire.
Il s'agit d'attribuer à un événement un nombre qui mesurera ses « chances » de réalisation.
Une idée naturelle est d'effectuer un grand nombre de fois l'expérience, et de compter le nombre de fois où l'événement est réalisé.
La fréquence de réalisation de l'événement donne ainsi une idée de ses chances de réalisation lors d'une prochaine expérience. On verra ultérieurement la validité de cette idée.
Mais ce n'est pas toujours possible de répéter l'expérience, et même si c'est possible, on ne peut pas en calculer la limite.
Cependant cette idée conduit à reprendre les propriétés de la fréquence statistique pour définir une probabilité.
Définition :
Une probabilité
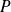sur l'espace probabilisable
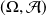est une application de la tribu des événements
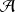dans
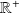qui vérifie :
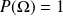.Pour toute suite
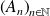d'éléments de
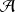deux à deux incompatibles :
.
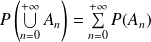Lorsque l'univers est fini, le deuxième axiome peut se réduire à deux événements incompatibles
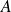et
:
.
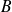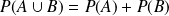Fondamental :
Propriétés
.
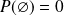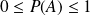pour tout événement
.
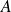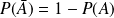pour tout événement
.
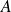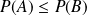pour tous les événements
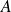et
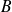tels que
.
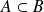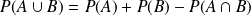pour tous les événements
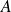et
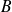.Formule du crible :
.
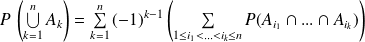La formule du crible est la généralisation de la propriété précédente.
Par exemple, dans le cas de trois événements, la formule du crible donne :
.
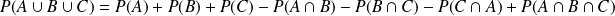Fondamental :
Propriétés de continuité monotone
Si
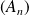est une suite croissante (
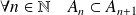) d'éléments de
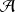, alors :
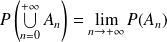.Si
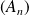est une suite décroissante (
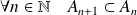) d'éléments de
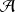, alors :
.
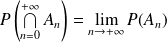C'est une propriété de « continuité » car, par exemple, lorsque la suite d'événements est croissante :
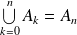, donc cela revient à dire que :
.
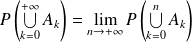Définition :
Un espace probabilisé
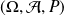est la donnée de l'univers
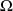, d'une tribu
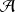d'événements et d'une probabilité
.
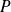La probabilité dépend des informations que l'on possède.
Dans le cas où
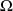est un univers fini ou infini dénombrable, on prend en général pour tribu d'événements
.
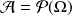Fondamental :
Cas d'un univers fini ou infini dénombrable
Si
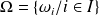où
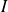est un ensemble fini ou infini dénombrable, la probabilité
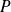est déterminée par les probabilités des événements élémentaires
:
-
.
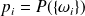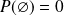Si
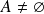, alors
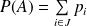où
.
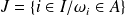Réciproquement une famille de nombres
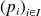définit une probabilité sur
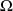si et seulement si :
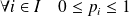et
.
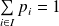Définition :
Equiprobabilité dans le cas d'un univers fini
Si
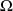est un univers fini, il y a équiprobabilité sur
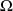si tous les événements élémentaires ont même probabilité.
Alors :
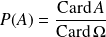pour tout événement
.
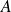En effet, tous les
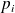sont égaux et leur somme vaut
, donc ils sont tous égaux à
.
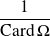L'équiprobabilité correspond à un « choix au hasard », ou à un manque d'information.
Attention :
Bien sûr, la notion d'équiprobabilité n'a de sens que si l'univers est un ensemble fini.
