Probabilité conditionnelle
Dans cette partie, on considère un espace probabilisé
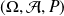associé à une expérience aléatoire.
Comme la probabilité dépend des informations que l'on possède, une information complémentaire ou une supposition change la probabilité.
Définition :
Probabilité conditionnelle
Soit
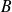un événement de probabilité
.
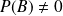Alors l'application
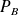qui, à tout élément
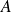de
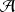, associe le réel positif
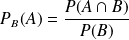est une probabilité sur
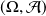, appelée probabilité conditionnée par
.
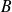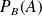est la probabilité que l'événement
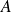se réalise, sachant que l'événement
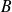est réalisé.
L'application
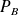est une probabilité, donc on en déduit :
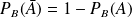pour tout événement
.
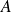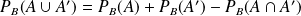pour tous les événements
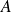et
.
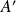Attention :
Attention à ne pas confondre
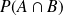et
.
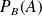La nuance n'est pas toujours facile à voir dans le langage courant.
Fondamental :
Formule des probabilités composées
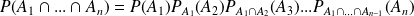si pour tout
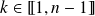, on a
.
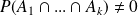En particulier :
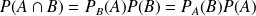si
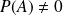et
.
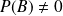Cette formule se déduit directement de la définition d'une probabilité conditionnelle.
Elle permet d'établir un lien entre les probabilités conditionnelles
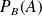et
.
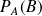Définition :
Système complet d'événements
Une famille
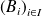d'éléments de
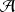est un système complet d'événements s'ils sont deux à deux incompatibles (
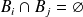si
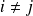), si leur réunion est
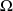et si
.
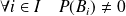En particulier, un événement
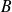de probabilité
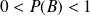et son contraire
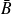forment un système complet d'événements.
Un système complet d'événements est une partition de l'univers
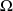, ce qui permet de construire une partition de tous les événements
.
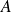Fondamental :
Formule des probabilités totales
Si
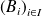est un système complet d'événements, alors :
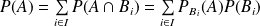pour tout événement
.
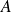En particulier, si
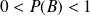, alors pour tout événement
:
.
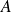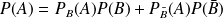Fondamental :
Formule de Bayes
Si
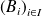est un système complet d'événements :
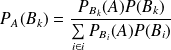pour tout événement
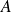tel que
.
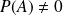Si les
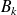représentent les causes possibles d'un événement
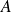, cette formule permet de calculer la probabilité de chaque cause lorsque l'événement
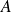est réalisé.
Par exemple lorsqu'un accident de voiture s'est produit, est-ce un problème de frein, un problème de direction, une faute du conducteur, ... ?
Dans le cas où le système complet d'événements est
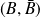, la formule devient :
.
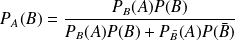