Evénements
Dans cette partie, on considère une expérience aléatoire et l'univers
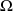qui lui est associé.
Il s'agit d'évaluer les « chances » de réalisation de certaines propriétés.
Définition :
Un événement
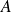est une partie de l'univers
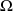. Il est réalisé pour l'éventualité
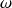si
.
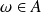Fondamental :
Vocabulaire des événements
L'événement impossible est :
.L'événement certain est :
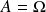.Un événement
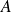est élémentaire s'il n'a qu'un seul élément :
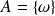.L'événement
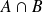est réalisé si les événements
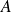et
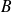sont réalisés. Si
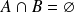, les événements
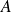et
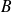sont incompatibles.L'événement
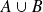est réalisé si l'événement
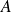ou l'événement
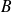est réalisé.L'événement
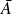est l'événement contraire de l'événement
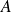.L'événement
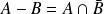est réalisé si l'événement
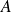est réalisé, mais pas l'événement
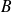.L'événement
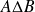est réalisé si l'un seulement des événements
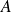ou
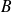est réalisé.
Cependant, on ne s'intéresse pas toujours à toutes les parties de
.
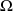Soit, par exemple, une urne qui contient
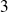boules rouges numérotées de
à
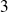, et deux boules vertes numérotées
et
.
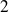On tire une boule dans cette urne, donc l'univers est :
.
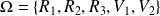Si l'on ne s'intéresse qu'à la couleur de la boule, il suffit de considérer :
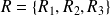et
.
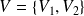Si l'on ne s'intéresse qu'au numéro, il suffit de considérer :
,
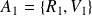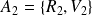et
.
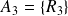Pour des questions de cohérence, certaines règles sont nécessaires.
Définition :
On appelle tribu (ou
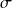- algèbre) d'événements toute partie
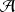de
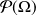qui vérifie :
elle contient l'univers :
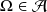.elle est stable par passage au complémentaire :
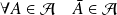.elle est stable par réunion dénombrable :
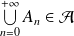pour toute suite
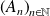d'éléments de
.
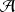L'événement
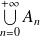est réalisé si l'un au moins des événements
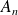est réalisé.
La plus « petite » tribu, ou « tribu grossière » est :
.
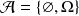La plus « grosse » tribu, ou « tribu discrète » est :
.
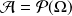La tribu engendrée par une famille de parties de
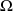est la plus petite tribu contenant cette famille.
Par exemple, la tribu engendrée par un événement
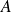est :
.
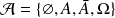Fondamental :
Propriétés des tribus
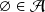.Si
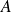et
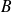sont des éléments de
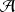, alors les événements
,
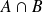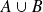et
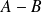appartiennent à
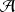.Pour toute suite
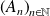d'éléments de
:
.
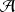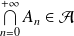L'événement
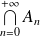est réalisé si tous les événements
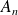sont réalisés.
Définition :
Un espace probabilisable
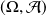associé à une expérience aléatoire est la donnée de l'univers
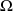et d'une tribu
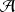d'événements.
Lorsque l'univers
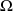est fini, on utilise le plus souvent la tribu :
.
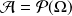