Expérience aléatoire
Le calcul des probabilités a été élaboré en relation avec des situations externes aux mathématiques, le but étant une prévision d'événements futurs et une aide à la prise de décision (tarif d'assurance vie, évaluation d'un risque, transmission d'un caractère génétique, nombre de lignes téléphoniques à installer,...).
Ces situations sont d'abord éventuellement simulées, puis modélisées.
Définition :
Une expérience aléatoire est une expérience dont le résultat dépend du hasard, c'est-à-dire ne peut être prévu avec certitude avant sa réalisation avec les informations dont on dispose.
Dans le mot expérience, il y a également deux choses implicites :
la réalisation doit obéir à un certain protocole défini de manière précise (par exemple, si l'on jette un dé, on n'acceptera pas que le dé soit « cassé »).
la réalisation peut être refaite autant de fois que l'on veut.
Ce dernier point peut être complètement irréaliste : destruction de l'objet. Dans ce cas, l'expérience est seulement imaginée ou simulée et on se base sur un raisonnement et non pas sur une constatation.
Comme on ne peut pas prévoir exactement le résultat avant de l'avoir réalisée, on commence par recenser tout ce qui peut arriver, tout ce qui est observable.
Définition :
On appelle éventualité tout résultat possible à priori de l'expérience.
L'ensemble
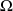de toutes les éventualités s'appelle l'univers des possibles ou des éventualités ou l'espace fondamental.
Exemple 1 : On lance un dé et il doit tomber sur une face.
L'univers est :
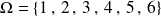. C'est un ensemble fini.
Exemple 2 : On lance une pièce jusqu'à ce que l'on obtienne Pile.
L'univers
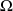est l'ensemble des suites de la forme
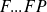avec
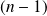fois « Face » pour tout entier non nul
. C'est un ensemble infini, mais dont on peut numéroter les éventualités.
L'univers
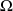est infini « dénombrable ».
Exemple 3 : Durée de vie d'un individu dans une population (personne ou objet).
L'univers
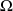est une partie de
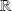, donc infini et non dénombrable.
L'étude sera différente selon que l'univers est fini, infini dénombrable ou infini non dénombrable.
Parfois, plusieurs descriptions sont possibles pour une même expérience aléatoire.
