Loi de probabilité
On considère un espace probabilisé
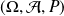et une variable aléatoire discrète finie
.
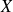Définition :
Soit
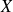une variable aléatoire discrète finie d'univers image
.
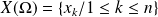La loi de probabilité de
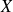est l'ensemble des réels
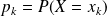pour tout
.
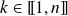Propriété :
.
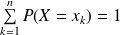En effet, les événements
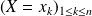forment un système complet d'événements.
La tribu engendrée par ces événements est appelée tribu associée à
.
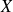On reprend l'exemple déjà étudié.
Exemple :
Exemple : Dans un sac qui contient
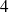jetons numérotés
,
,
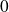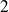et
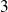, on tire successivement (sans remise) deux jetons et
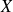est la somme des deux numéros obtenus.
Déterminer la loi de probabilité de la variable aléatoire
.
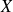Lorsque l'univers image n'a que peu d'éléments, on résume la loi de probabilité dans un tableau :
Fondamental :
Soit
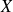une variable aléatoire discrète finie d'univers image
.
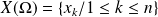Soit
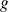une application de
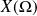dans
.
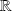La variable
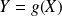a pour univers image :
.
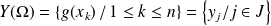Sa loi de probabilité est :
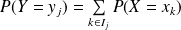où
.
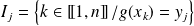Par exemple, si
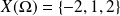et
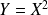, alors :
.
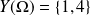La loi de
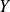est définie par :
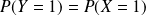et
.
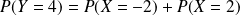Définition :
La fonction de répartition de la variable aléatoire
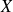est la fonction définie par :
.
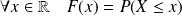Cette notion correspond à celle des fréquences cumulées croissantes en statistique.
Fondamental :
Propriétés :
La fonction de répartition est une fonction en escalier croissante.
Elle est continue à droite en tout réel
.Elle admet pour limites :
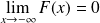et
.
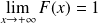Elle permet d'exprimer les probabilités de divers événements.
Pour tous
et
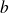réels, on a :
.
.
.
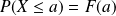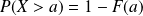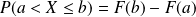Méthode :
Détermination pratique :
On suppose que l'univers image est
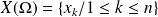avec
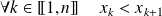et
.
.
.
.
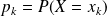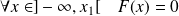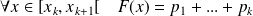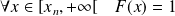Dans certains cas, il est plus facile de déterminer la fonction de répartition et d'en déduire la loi de probabilité.
En effet, la loi de probabilité de
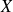peut s'exprimer à l'aide de la fonction de répartition :
.
.
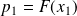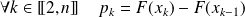