Espérance mathématique d'une variable aléatoire discrète finie
On considère un espace probabilisé
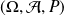 .
.
Soit
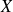 une variable aléatoire discrète finie d'univers image
une variable aléatoire discrète finie d'univers image
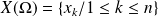 et pour laquelle on pose :
et pour laquelle on pose :
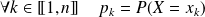 .
.
Définition :
On appelle espérance mathématique de
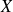 le réel :
le réel :
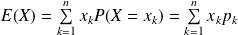 .
.
L'espérance mathématique correspond à la notion de moyenne statistique : c'est la valeur « moyenne » prise par la variable aléatoire
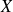 .
.
On reprend l'exemple déjà étudié.
Exemple :
Exemple
On a vu que la loi de probabilité de la variable aléatoire
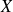 est :
est :
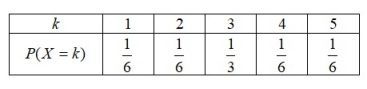
Déterminer son espérance mathématique.
Fondamental :
Propriétés :
Soit
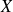 une variable aléatoire réelle d'univers image
une variable aléatoire réelle d'univers image
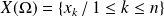 et de loi définie par :
et de loi définie par :
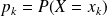 .
.
Si
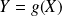 , alors :
, alors :
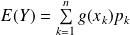 (Théorème de transfert)
(Théorème de transfert)
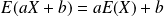 pour tous réels
pour tous réels
 et
et
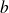 .
.Si
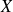 et
et
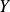 sont deux variables aléatoires discrètes finies, alors :
sont deux variables aléatoires discrètes finies, alors :
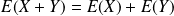 .
.
Par exemple :
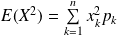 .
.
L'application qui, à toute variable aléatoire discrète finie, associe son espérance est linéaire.
Définition :
Une variable aléatoire
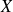 est centrée si son espérance est nulle.
est centrée si son espérance est nulle.
En particulier, un jeu est équitable si la variable aléatoire mesurant le gain est centrée.
On peut remarquer que pour toute variable aléatoire discrète finie
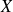 , si
, si
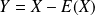 , alors :
, alors :
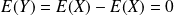 .
.
La variable aléatoire
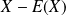 est appelée variable aléatoire centrée associée à X.
est appelée variable aléatoire centrée associée à X.
Fondamental :
Inégalité de Markov
Soit
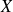 une variable aléatoire discrète finie ne prenant que des valeurs positives ou nulles.
une variable aléatoire discrète finie ne prenant que des valeurs positives ou nulles.
Alors :
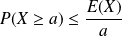 pour tout réel
pour tout réel
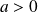 .
.
Cette inégalité n'a d'intérêt que si
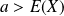 puisque l'on sait que la probabilité est majorée par
puisque l'on sait que la probabilité est majorée par
 .
.
Par exemple, la probabilité que
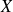 soit plus grande que
soit plus grande que
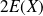 est plus petite que
est plus petite que
 .
.





