Variance et écart-type
On considère un espace probabilisé
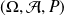 .
.
Soit
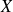 une variable aléatoire discrète finie d'univers image
une variable aléatoire discrète finie d'univers image
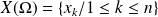 et pour laquelle on pose :
et pour laquelle on pose :
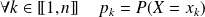 .
.
Définition :
Pour toute variable aléatoire discrète finie
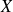 et tout entier naturel
et tout entier naturel
 , on appelle moment d'ordre r de
, on appelle moment d'ordre r de
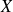 l'espérance de la variable
l'espérance de la variable
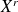 .
.
Le moment d'ordre
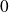 de
de
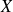 est égal à
est égal à
 .
.
Le moment d'ordre
 de
de
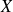 est son espérance.
est son espérance.
Définition :
On appelle variance de
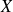 le moment d'ordre
le moment d'ordre
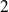 de la variable aléatoire centrée associée à
de la variable aléatoire centrée associée à
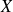 .
.
La variance de
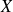 est donc le réel :
est donc le réel :
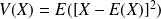 .
.
Comme en statistiques, elle mesure la dispersion de
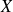 autour de sa "valeur moyenne"
autour de sa "valeur moyenne"
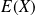 .
.
Fondamental :
Propriétés
Soit
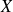 une variable aléatoire réelle discrète finie :
une variable aléatoire réelle discrète finie :
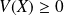 .
.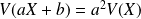 pour tous réels
pour tous réels
 et
et
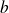 .
.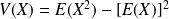 (Théorème de Koenig-Huygens).
(Théorème de Koenig-Huygens).
C'est cette dernière expression qui est le plus souvent utilisée pour calculer la variance.
On reprend l'exemple étudié précédemment.
Exemple :
Exemple
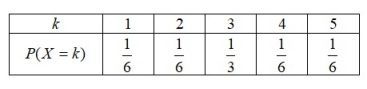
On a vu que la loi de probabilité de la variable aléatoire
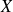 est :
est :
Définition :
L'écart-type d'une variable aléatoire discrète finie
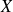 est le réel :
est le réel :
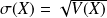 .
.
Propriété :
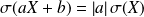 pour tous réels
pour tous réels
 et
et
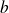 .
.
On retrouve la définition de l'écart-type en statistiques.
Définition :
Une variable aléatoire
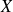 est centrée réduite si
est centrée réduite si
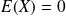 et
et
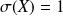 .
.
On peut remarquer que pour toute variable aléatoire discrète finie
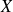 , si
, si
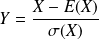 , alors :
, alors :
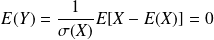 et
et
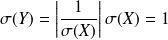 .
.
La variable aléatoire
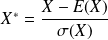 est appelée variable aléatoire centrée réduite associée à X.
est appelée variable aléatoire centrée réduite associée à X.
Fondamental :
Inégalité de Bienaymé-Tchebychev
Soit
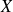 une variable aléatoire discrète finie.
une variable aléatoire discrète finie.
Alors :
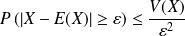 pour tout
pour tout
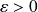 .
.
Cette inégalité n'a d'intérêt que si
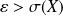 puisque l'on sait que la probabilité est majorée par
puisque l'on sait que la probabilité est majorée par
 .
.
Par exemple, la probabilité que
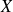 s'écarte de sa moyenne de plus de
s'écarte de sa moyenne de plus de
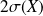 est plus petite que
est plus petite que
 .
.
Cela signifie qu'il y a au moins
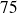 % de chances que
% de chances que
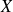 prenne ses valeurs dans l'intervalle
prenne ses valeurs dans l'intervalle
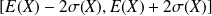 .
.