Variables aléatoires discrètes finies
Dans tout ce qui suit, on considère un espace probabilisé
.
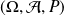Définition :
Une variable aléatoire réelle
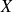sur
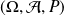est une application de
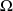dans
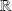telle que pour tout intervalle
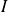de
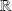, on ait
.
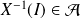Si la tribu des événements est
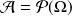, toute application de
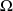dans
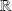est une variable aléatoire réelle.
Définition :
L'univers image de la variable aléatoire
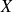est l'ensemble
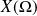des valeurs prises par
.
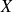La variable aléatoire est discrète finie si son univers image
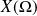est un ensemble fini.
C'est en particulier le cas si l'ensemble
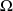est fini.
Exemple :
Exemple : Dans un sac qui contient
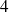jetons numérotés
,
,
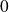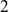et
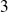, on tire successivement (sans remise) deux jetons et
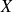est la somme des deux numéros obtenus.
L'univers
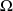est l'ensemble des couples
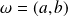tels que
et
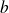appartiennent à
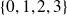avec
.
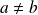Et
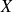est l'application qui au couple
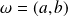associe le réel
.
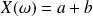Son univers image est donc :
.
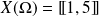La variable aléatoire
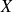est donc une variable aléatoire discrète finie.
Fondamental :
Opérations sur les variables aléatoires
Si
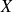est une variable aléatoire discrète finie et si
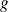est une application de
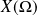dans
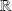, l'application
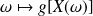est une variable aléatoire discrète finie notée
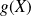.Si
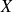et
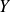sont deux variables aléatoires discrètes finies, l'application
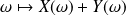est une variable aléatoire discrète finie notée
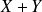.Si
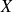et
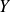sont deux variables aléatoires discrètes finies, l'application
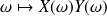est une variable aléatoire discrète finie notée
.
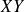Dans l'exemple précédent, la variable
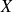est la somme des variables
:
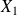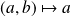et
:
.
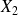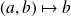Remarque :
Notations
On abrège l'écriture de certains événements liés à
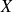. Par exemple, si
et
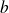sont des réels :
.
.
.
.
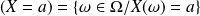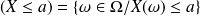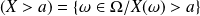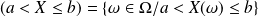