Lois discrètes finies usuelles
Il s'agit de repérer quelques situations souvent rencontrées pour éviter de refaire à chaque fois les calculs d'espérance et variance.
On se place toujours dans un espace probabilisé
.
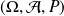Fondamental :
Une variable aléatoire
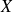est certaine si elle est constante, donc s'il existe un réel
tel que
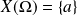et
.
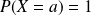Son espérance est
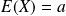et sa variance est
.
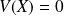C'est évidemment la plus simple, mais elle n'est utilisée que comme outil.
Fondamental :
Une variable aléatoire
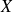suit la loi discrète uniforme de paramètre
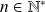si son univers image est
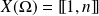et si
.
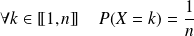On note
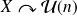ou
.
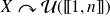Son espérance est
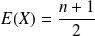et sa variance est
.
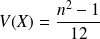Cette loi correspond à la situation d'équiprobabilité pour un tirage d'un objet parmi
.
On en déduit une loi discrète uniforme sur tout intervalle
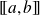où
et
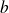sont des entiers naturels avec
.
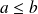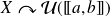si l'univers image est
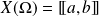et si
.
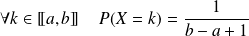Son espérance est
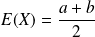et sa variance est
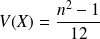où
.
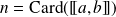Fondamental :
Une variable aléatoire discrète
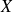suit la loi de Bernoulli de paramètre
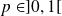si son univers image est
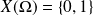avec
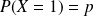et
.
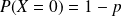On note
.
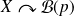Son espérance est
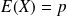et sa variance est
.
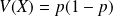Cette loi intervient lorsqu'une situation n'a que deux issues : succès et échec.
Une telle situation s'appelle une épreuve de Bernoulli.
Fondamental :
Une variable aléatoire discrète
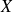suit la loi binomiale de paramètres
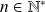et
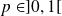si son univers image est
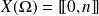et si
.
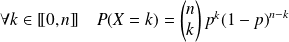On note
.
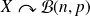Son espérance est
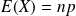et sa variance est
.
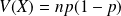C'est la loi du nombre de succès dans un schéma de Bernoulli, c'est-à-dire une succession de
épreuves de Bernoulli indépendantes et de même probabilité de succès
.
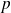Par exemple, si l'on lance
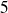fois de suite une pièce qui amène pile avec la probabilité
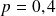, le nombre
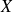de piles obtenus suit la loi
.
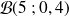Donc :
.
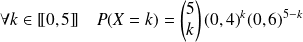Fondamental :
Une variable aléatoire discrète
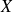suit la loi hypergéométrique de paramètres
,
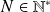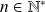et
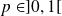avec
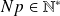si son univers image est
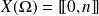et si
.
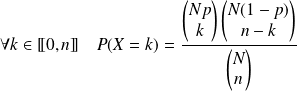On note
.
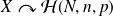Son espérance est
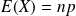et sa variance est
.
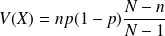Cette loi intervient dans le cas de tirages sans remise.
Dans une urne qui contient
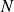boules avec une proportion
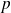de boules blanches (il y a donc
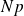boules blanches), si l'on tire successivement sans remise
boules, alors le nombre de boules blanches obtenues suit la loi hypergéométrique
.
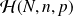On peut montrer qu'on a le même résultat si l'on tire simultanément les
boules.
Par exemple, si l'on tire
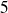boules, successivement sans remise ou simultanément, dans une urne qui contient
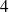boules blanches et
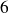boules noires, le nombre
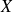de boules blanches obtenues suit la loi hypergéométrique
.
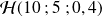Donc :
.
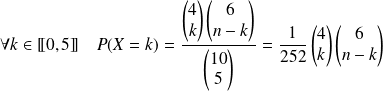Bien sûr, comme il n'y a que
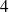boules blanches, on a
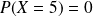puisque
.
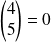