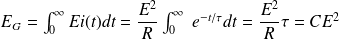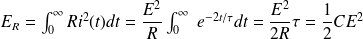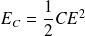Régimes transitoires dans les circuits RC, RL et RLC
Fondamental : Charge et décharge d'un condensateur, étude du circuit (R,C)
Un condensateur est assimilable à deux plaques disposées face à face.
En règle générale, on pourra dire qu'un condensateur est constitué de deux conducteurs séparés par un isolant (appelé également diélectrique).
Cet isolant peut être l'air, du verre, du plastique ...
Les condensateurs sont utilisés dans pratiquement tous les montages électroniques.
Par exemple, on utilise des condensateurs variables dans les circuits d'accord de postes de radio.
Soumis à une tension
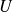 , un condensateur possède la propriété de se charger et de conserver une charge électrique
, un condensateur possède la propriété de se charger et de conserver une charge électrique
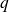 , proportionnelle à
, proportionnelle à
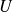 :
:
C'est un réservoir d'énergie.
On peut comparer le condensateur à un réservoir qui se remplit et se vide, ou à un poumon qui se gonfle et se dégonfle...
Cette énergie est restituée lors de la décharge du condensateur (flashs électroniques, par exemple).
Ces phénomènes de charge et de décharge ne sont pas instantanés ; ce sont des phénomènes transitoires.
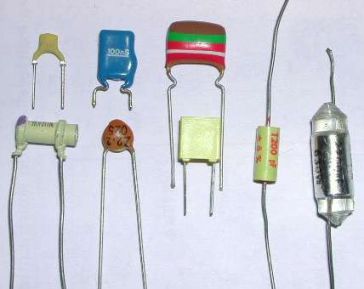
Avec les notations de la figure suivante :
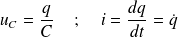
La puissance reçue par le condensateur (de manière algébrique) est :
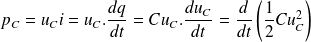
L'énergie EC emmagasinée par le condensateur s'en déduit :
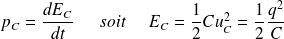
La charge portée par les armatures est une fonction continue du temps.
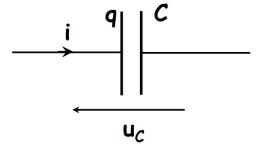
Charge d'un condensateur par un échelon de tension :
On choisit :
A
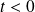 :
:
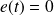 et à
et à
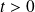 :
:
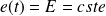 .
.
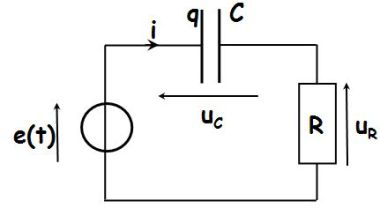
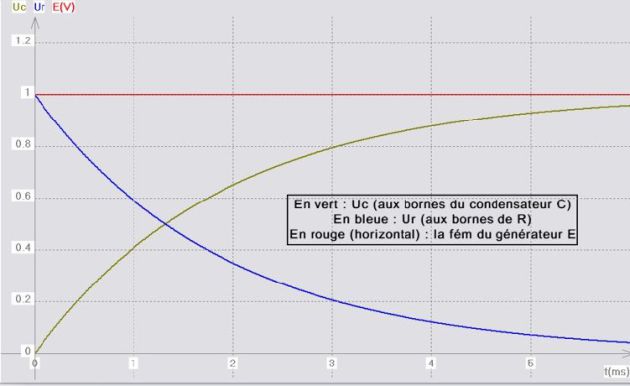
Alors, pour
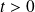 :
:

Et :
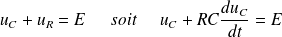
Ou encore :
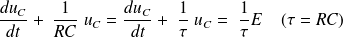
Si le condensateur est déchargé à
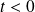 :
:
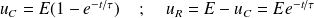
 est la constante de temps du circuit (RC) : elle donne l'ordre de grandeur de la durée de charge du condensateur. \
est la constante de temps du circuit (RC) : elle donne l'ordre de grandeur de la durée de charge du condensateur. \
La charge est continue à
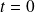 ; l'intensité est discontinue (passe de
; l'intensité est discontinue (passe de
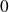 à
à
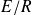 de
de
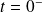 à
à
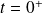 ).
).
Aspect énergétique :
Que devient l'énergie fournie par le générateur ? D'après la conservation de l'énergie, on va montrer que :
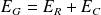
Avec :
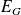 : énergie fournie par le générateur
: énergie fournie par le générateur 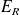 : énergie dissipée par effet Joule dans R
: énergie dissipée par effet Joule dans R 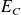 : énergie emmagasinée par C
: énergie emmagasinée par C
On calcule :
D'où :

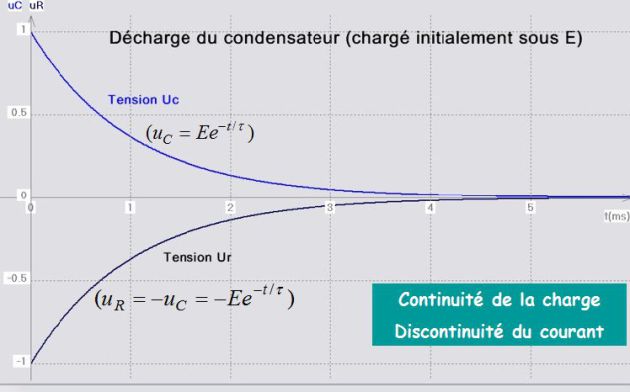
Décharge du condensateur :
La figure suivante illustre les résultats.
Fondamental : Bobine d'auto-induction, étude du circuit (R,L)
Tout bobinage parcouru par un courant crée un champ magnétique proportionnel à l'intensité i.
Lorsque l'intensité i dépend du temps, il apparaît aux bornes de la bobine une fém d'auto-induction (phénomène d'induction).
En convention récepteur, cette fém s'écrit (en supposant la bobine idéale, c'est-à-dire sans résistance) :
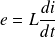
Le rôle d'une bobine d'auto-induction est de s'opposer à toute modification du courant dans un circuit (loi de Lenz).
En particulier, l'intensité du courant dans une bobine est nécessairement continue.
Tension, puissance et énergie :
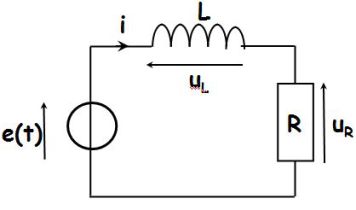
Avec les notations de la figure suivante :

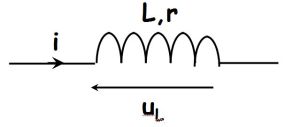
La puissance reçue par la bobine (de manière algébrique) est (bobine idéale ici, soit r = 0) :

L'énergie
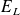 emmagasinée par la bobine s'en déduit :
emmagasinée par la bobine s'en déduit :
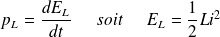
L'intensité du courant qui traverse une bobine est une fonction continue du temps.
Réponse à un échelon de tension (bobine idéale) :
On choisit :
A
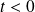 :
:
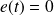 et à
et à
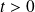 :
:
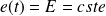 .
.
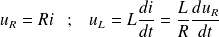
Et :
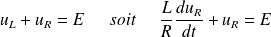
Soit :
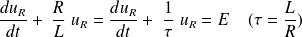
Si l'intensité du courant est nulle à
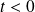 :
:

 est la constante de temps du circuit (RL) : elle donne l'ordre de grandeur de la durée d'établissement du régime permanent (
est la constante de temps du circuit (RL) : elle donne l'ordre de grandeur de la durée d'établissement du régime permanent (
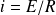 ).
).
La bobine se comporte ensuite comme un simple fil.
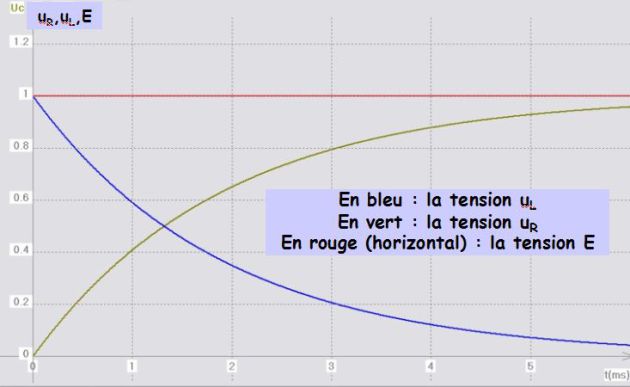
L'intensité (et la tension
 ) est continue à
) est continue à
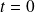 ; la tension
; la tension
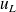 est discontinue (passe de 0 à E de
est discontinue (passe de 0 à E de
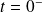 à
à
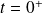 ).
).
Aspect énergétique :
On va montrer que :
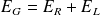
Avec :
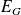 : énergie fournie par le générateur
: énergie fournie par le générateur 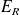 : énergie dissipée par effet Joule dans R
: énergie dissipée par effet Joule dans R 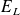 : énergie emmagasinée par la bobine
: énergie emmagasinée par la bobine
En effet :
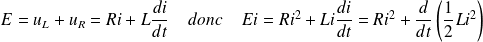
D'où le résultat :

Fondamental : Régimes transitoires dans un circuit série (RLC)
Équation différentielle du circuit (RLC) :
La loi des mailles donne :
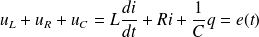
Or :
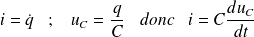

Ainsi :

Soit :
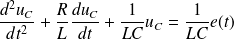
Ou encore :
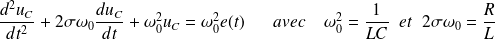
Les différents régimes :
On recherche des solutions de l'équation homogène de la forme
 , avec
, avec
 appartenant a priori au corps des complexes.
appartenant a priori au corps des complexes.
On aboutit au polynôme caractéristique :

Dont le discriminant est :
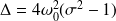
Alors :
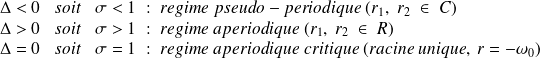
Il faut ensuite rajouter une solution particulière, qui dépend de la forme de e(t).
Réponse du circuit (RLC) à un échelon de tension :
Pour
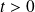 :
:
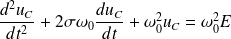
La solution de l'équation différentielle précédente est alors :

Au bout de
 , le régime permanent est atteint (
, le régime permanent est atteint (
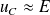 ).
).
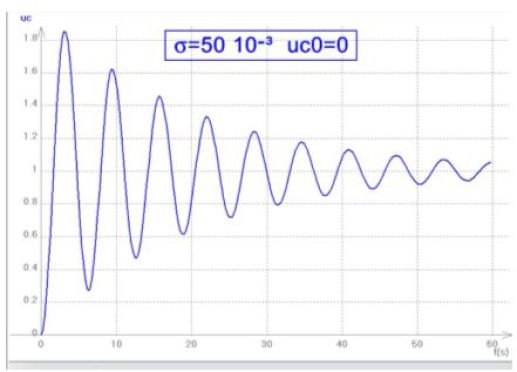
Aspect énergétique :
L'état final est :
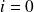 et
et
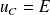 (le condensateur est chargé).
(le condensateur est chargé).
Montrons que le bilan final énergétique s'écrit :

Avec :
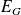 : énergie fournie par le générateur
: énergie fournie par le générateur 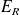 : énergie dissipée par effet Joule dans R
: énergie dissipée par effet Joule dans R 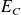 : énergie emmagasinée par C
: énergie emmagasinée par C
En effet :

Et :
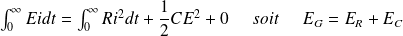
On peut calculer l'énergie fournie par le générateur :
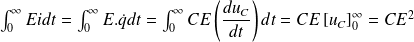
On en déduit que l'énergie dissipée par effet Joule dans la résistance R vaut :
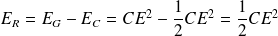
Par conséquent :
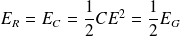
La moitié de l'énergie fournie par le générateur est dissipée par effet Joule.
On retrouve le même résultat que dans le cas du circuit (RC) : ce n'est pas surprenant puisque l'inductance n'a aucune influence sur les états initial et final du circuit.
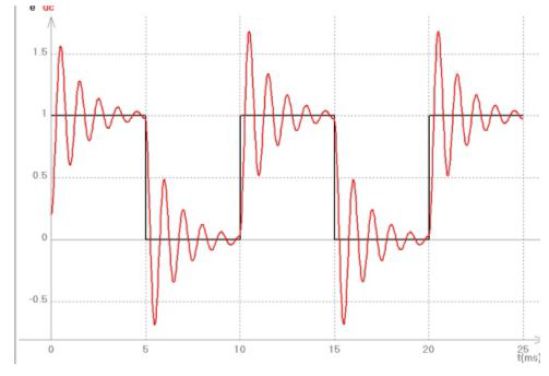
Réponse à une tension créneau :