Analyse de Fourier et électronique
(Voir également la fiche expérimentale consacrée à l'analyse spectrale)
Fondamental : Décomposition en séries de Fourier
Un signal périodique
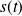de période
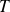peut (sous certaines conditions qui sont supposées être vérifiées en physique), se décomposer en une somme de fonctions sinusoïdales (décomposition en séries de Fourier) :
Les coefficients
,
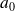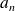et
sont constants et donnés par les intégrales :
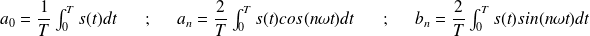
On remarque que le coefficient
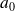représente la valeur moyenne de
.
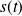Le terme correspondant à
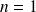(soit une pulsation égale à celle du signal
) :
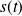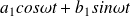
est appelé le fondamental.
Le terme général
est l'harmonique de rang
.
Signal
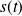pair et signal impair :
Si
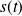est impair (
: Le développement en séries de Fourier du signal
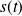ne comprend alors que des termes en sinus (les coefficients
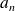sont nuls) :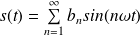 
Si
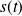est pair (
: Le développement en séries de Fourier du signal
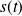ne comprend alors que des termes en cosinus (les coefficients
sont nuls) : 
Spectre en fréquences :
Le terme général
peut être mis sous la forme :
Si l'on pose :
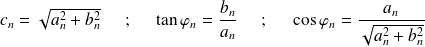
Alors :
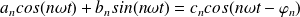
Et le signal périodique
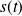devient :
Le spectre en fréquences (ou encore représentation spectrale) du signal
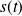est obtenu en portant en ordonnée l'amplitude des harmoniques (c'est-à-dire les coefficients
,
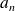ou
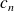) et en abscisse les pulsations correspondantes.
Exemple : Quelques signaux particulièrs
Signal carré :
La tension créneaux (ou tension carrée)
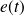de la figure suivante peut se décomposer en séries de Fourier sous la forme :
C'est une fonction impaire. Par conséquent, le développement en séries de Fourier ne comprend pas de termes en cosinus.
On remarque que les harmoniques sont de rang impair (de la forme
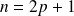) et que les coefficients
diminuent comme
.
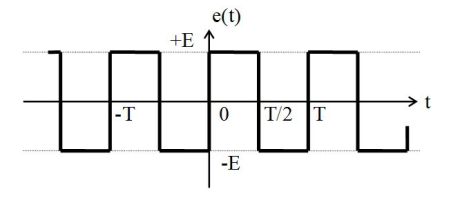
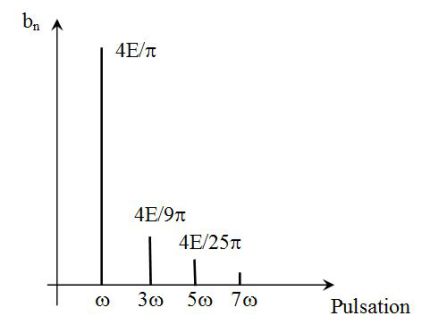
La figure suivante donne le spectre en fréquences de ce signal carré.
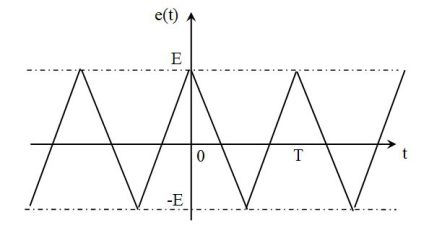
Signal triangulaire :
La tension triangulaire
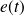de la figure suivante peut s'écrire :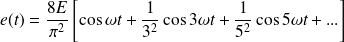
C'est une fonction paire. Par conséquent, le développement en séries de Fourier ne comprend pas de termes en sinus.
On remarque que les harmoniques sont de rang impair (de la forme
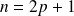) et que les coefficients
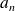diminuent comme
.
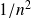La figure suivante donne le spectre en fréquences de ce signal carré.
Des animations Java (Par JJ Rousseau, Université du Mans) :
Des animations sur la décomposition en séries de Fourier de fonctions classiques : carré, triangulaire, rampe, demi-sinus et impulsion :
Cliquer ICI
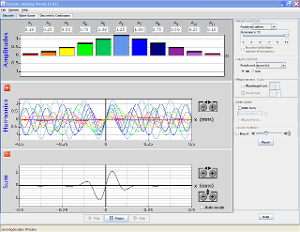
Synthèse de Fourier : cette applet permet de visualiser les résultats de la synthèse de Fourier.
Elle génère également le signal sonore correspondant :
Cliquer ICI
Complément : Valeur moyenne, valeur efficace, formule de Parseval et facteur de forme d'un signal
Soit un signal
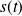périodique, dont la décomposition en séries de Fourier s'écrit :
La valeur moyenne de
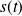est :
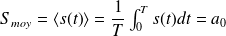
La valeur efficace vaut :
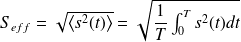
En utilisant la décomposition en séries de Fourier :
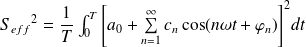
Sachant que la valeur moyenne d'une fonction sinusoïdale est nulle, que la valeur moyenne d'un produit de deux fonctions sinusoïdales de pulsations différentes est nulle et que la valeur moyenne d'un sinus au carré est
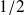, il vient :
C'est la formule de Parseval : "Le carré de la valeur efficace d'un signal périodique est égal à la somme du carré de sa valeur moyenne et des carrés des valeurs efficaces des harmoniques".
Deux cas particuliers :
Si
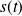est un signal sinusoïdal pur :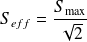 
Si
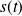est un signal sinusoïdal décalé par une composante continue :
Le facteur de forme (noté
) d'un signal périodique
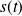est le rapport entre la valeur efficace et la valeur moyenne du signal :
Pour un signal continu :
. -
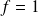n'est pas défini pour un signal périodique de valeur moyenne nulle.
Pour un signal sinusoïdal redressé double alternance :
Complément : Distorsion harmonique
On considère un système électrique non linéaire : lorsque la tension d'entrée est sinusoïdale, la tension de sortie ne l'est pas ou présente une pulsation différente de celle de l'entrée.
On réalise alors une décomposition harmonique du signal de sortie (dans l'hypothèse où celui-ci est périodique) :
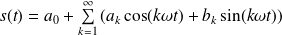
Si le système était rigoureusement linéaire, seuls les coefficients de degré 1 seraient non nuls.
Les termes d'ordre supérieur ou égal à 2 constituent la distorsion harmonique.
On appelle taux de distorsion harmonique, noté DHT et exprimé en dB, le rapport entre la puissance des termes harmoniques et celle du signal total :
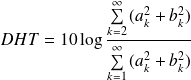
Pour un système linéaire, DHT tend vers
.
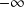Exemple :
La sortie est reliée à l'entrée par la relation :
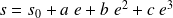
Avec :
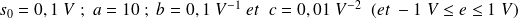
On suppose l'entrée sinusoïdale :
La sortie devient alors :
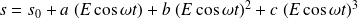
Avec :
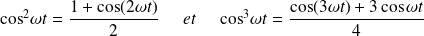
Il vient :
En supposant
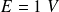, on obtient :
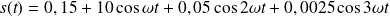
Le taux de distorsion harmonique vaut :
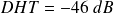
Une analyse harmonique (utilisant un analyseur de spectres, par exemple) permettrait de mettre en évidence ces non linéarités.
Fondamental : Critère de Nyquist-Shannon
Simulation : Des animations sur la décomposition en séries de Fourier
Des animations Java (Par JJ Rousseau, Université du Mans) :
Des animations sur la décomposition en séries de Fourier de fonctions classiques : carré, triangulaire, rampe, demi-sinus et impulsion :
Cliquer ICI
Synthèse de Fourier : cette applet permet de visualiser les résultats de la synthèse de Fourier.
Elle génère également le signal sonore correspondant :
Cliquer ICI
Simulation : Une animation sur la décomposition en séries de Fourier (Université du Colorado)
Apprenez à faire des ondes de toutes les formes différentes en ajoutant des sinus ou des cosinus.
Faire des ondes dans l'espace et le temps et mesurer leurs longueurs d'onde et leurs périodes.
Voyez comment changer les amplitudes des différentes harmoniques changent les ondes.
Comparer les différentes expressions mathématiques de vos ondes.
| Cliquer pour lancer |
