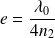Interfaces entre deux milieux
Définition : Diélectriques
Dans la matière, un champ EM agit sur les atomes, les molécules ou les ions en les déformant. Le milieu matériel va ainsi :
Se polariser sous l'action du champ électrique
S'aimanter sous l'action du champ magnétique
Dans certains milieux (métaux, plasmas), les charges se déplacent librement (on parle de charges et de courants libres).
Dans les diélectriques (ou isolants), les charges ne se déplacent que très peu et s'organisent sous forme essentiellement de dipôles électriques (on néglige les contributions dues à l'apparition de quadripôles ou même d'octopôles électriques).
Ces modifications vont alors provoquer l'apparition d'un champ électrique (ou magnétique) induit par le champ EM externe, qui s'ajoute à celui-ci.
Une erreur consiste à croire qu'un milieu isolant (comme les diélectriques) ne laisse pas passer les ondes (hertziennes par exemple).
Or c'est exactement le contraire : les diélectriques sont essentiellement transparents aux ondes hertziennes, alors que les milieux conducteurs (eau de mer, métaux) les réfléchissent et les absorbent.
Fondamental : Vitesse d'une onde EM dans un diélectrique
On définit l'indice d'un milieu diélectrique (comme le verre par exemple), sous la forme :
où
est la vitesse de la lumière dans le vide et
la vitesse de la lumière dans le milieu considéré.
Pour le verre,
est de l'ordre de 1,6 et pour l'eau,
est de l'ordre de 1,3.
Le vide possède évidemment un indice égal à 1 et l'air a un indice très proche de celui du vide.
Les équations de d'Alembert pour les champs EM deviennent alors, en remplaçant
par
:
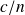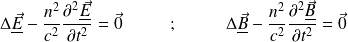
Méthode : Réflexion et réfraction des ondes EM : coefficients (en amplitude) de réflexion et de transmission en incidence normale
On considère deux milieux diélectriques (1) et (2).
On se place dans les zones de transparence pour lesquelles les indices des deux milieux
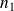et
sont réels.
Une onde incidente arrive à l'interface entre les deux milieux (sur le dioptre, surface qui sépare les deux diélectriques) en incidence normale.
On souhaite déterminer l'onde réfléchie et l'onde transmise.
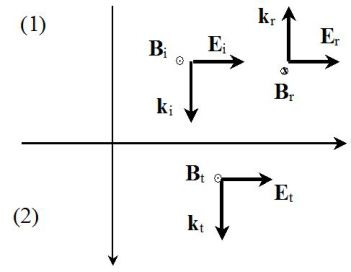
On suppose les ondes polarisées rectilignement :
On note les vecteurs d'onde (
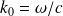est le vecteur d'onde dans le vide) :
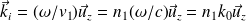
De même :
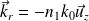
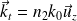
Expressions des champs électriques :
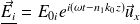
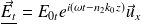
Expression des champs magnétiques :
On obtient les champs magnétiques en utilisant la relation de structure d'une onde plane.
Ainsi :
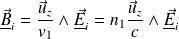
Soit, finalement :
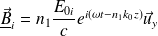
De même (l'onde réfléchie se propage selon
) :
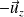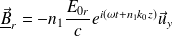
Et :
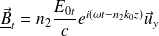
Les diélectriques sont non chargés. Dans une représentation volumique, il y a continuité des champs électriques et magnétiques à la traversée du dioptre en
.
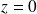Par conséquent, les conditions de passage pour les champs s'écrivent :
Pour le champ électrique :
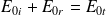
Pour le champ magnétique :
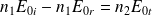
On en déduit :
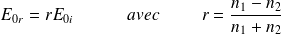
est le coefficient de réflexion en amplitude pour le champ électrique.
Et :
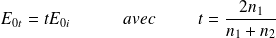
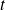est le coefficient de transmission en amplitude pour le champ électrique.
Quelques remarques :
t est toujours positif : il n'y a pas de changement de phase lors de la transmission.
r peut être positif ou négatif :
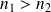: la réflexion n'introduit pas de déphasage
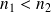: la réflexion introduit un déphasage de
.
Méthode : Coefficients (en énergie) de réflexion et de transmission en incidence normale :
Le vecteur de Poynting incident est (en valeur moyenne) :
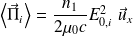
Pour les ondes réfléchie et transmise :
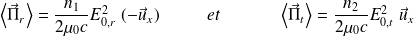
Les coefficients en énergie de réflexion et de transmission sont alors :
On vérifie la conservation de l'énergie :
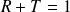
Une application numérique :
Dans le cas du dioptre air-verre (
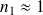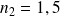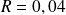et
) :
et
: l'énergie est pratiquement totalement transmise.
Exemple : Lame anti-reflet
Une OPPH polarisée rectilignement de longueur d'onde
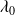dans le vide, provenant d'un milieu d'indice
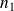arrive en incidence normale sur un milieu d'indice
et d'épaisseur
puis ressort dans un milieu d'indice
.
Comment choisir l'indice
pour qu'il n'y ait pas de réflexion dans le premier milieu ?
Les coefficients de réflexion et de transmission aux interfaces sont :
Interface milieu 1 - milieu 2 :
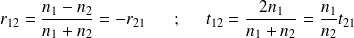
Interface milieu 2 - milieu 3 :
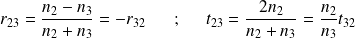
On note
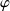le déphasage dû à la propagation dans la lame anti-reflet :
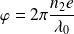
L'amplitude de l'onde réfléchie dans le milieu 1 peut alors s'écrire (
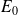est l'amplitude de l'onde incidente) :
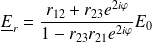
Il n'y aura pas d'onde réfléchie dans le milieu 1 si :
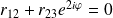
Les coefficients de réflexion étant réels, on en déduit que nécessairement :
(
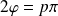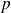entier naturel non nul)
La seule solution physiquement acceptable est obtenue pour
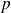impair.
On trouve :
Et l'épaisseur la plus faible possible pour la lame est :
