Ondes EM dans les plasmas
Définition : Définition d'un plasma
La matière telle qu'on la connaît sur Terre peut exister essentiellement sous trois formes bien familières : l'état solide, l'état liquide et l'état gazeux.
Il existe cependant un quatrième état de la matière, appelé plasma, obtenu lorsque la matière est portée par exemple à très haute température.
Paradoxalement, c'est cet état qui est, à l'échelle de l'Univers, le plus courant puisque les astrophysiciens estiment que 99% de la matière est à l'état de plasma dans l'Univers.
Un plasma est un milieu composé d'atomes ou de molécules partiellement ou complètement ionisés mais qui reste globalement électriquement neutre ; ainsi, un plasma d'hydrogène est composé d'atomes d'hydrogène, de protons (les noyaux d'hydrogène) et d'électrons libres, en proportions différentes selon la nature du plasma (plasma peu ou au contraire complètement ionisé).
Les particules chargées (ions et électrons) constituant le plasma interagissent par l'intermédiaire des forces électromagnétiques.
L'existence de ces forces à longue portée permet à une particule d'interagir avec beaucoup d'autres, ce qui donne un caractère collectif à ces interactions.
Ce caractère collectif a été notamment mis en évidence par des oscillations longitudinales étudiées en 1925 par Irwing Langmuir. Un certain volume d'électrons, déplacé de sa position d'équilibre, laisse un défaut de charge qui devient une charge d'espace positive ; il en résulte une force de rappel due au champ électrique qui tend à ramener les électrons à leur position d'équilibre.
La création d'un plasma nécessite un apport important d'énergie.
Celui-ci peut se faire par chauffage, par bombardement avec un faisceau laser très intense ou encore par décharge électrique dans un gaz soumis à une très forte différence de potentiel (dans des dispositifs connus sous le nom de tubes à décharges).
On distingue traditionnellement deux sortes de plasmas : les plasmas «froids» dont la température reste inférieure à
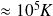et les «plasmas» chauds pour lesquels la température excède
.
Les exemples de plasmas dans la nature sont nombreux ; on peut citer :
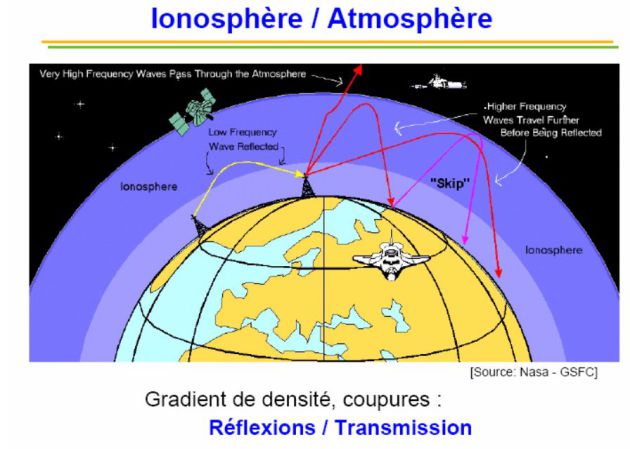
La magnétosphère et l'ionosphère terrestres.
Le cœur des étoiles, exemple de plasma chaud et très dense.
Les tubes à néon et le phénomène de la foudre (décharges électriques).
Les applications de la physique des plasmas sont très diverses et en plein développement, dans des domaines aussi variés que :
La fusion thermonucléaire : en réalisant un plasma de très forte densité et à très haute température, les physiciens espèrent amorcer des réactions de fusion nucléaire et créer ainsi un générateur d'énergie considérable.
L'électronique : l'utilisation de plasmas froids permet de réaliser des circuits électroniques intégrés. La télévision de l'avenir possédera certainement un écran à plasma.
Traitement des matériaux : les plasmas permettent de détruire, transformer, analyser, souder, créer...la matière. Par exemple, des fibres plastiques peuvent être traitées par plasma pour devenir imperméables.
Si l'apport d'énergie devient considérable, les noyaux des atomes peuvent se séparer en leurs constituants premiers, les nucléons (protons et neutrons) : le plasma obtenu est alors un mélange de nucléons et d'électrons.
A plus haute énergie encore (lors par exemple de collisions réalisées à des vitesses pratiquement égales à celle de la lumière entre noyaux atomiques), les nucléons peuvent se désintégrer en leurs constituants ultimes, les quarks et les gluons (particules responsables de la cohésion des quarks au sein des noyaux atomiques). La «soupe» ainsi obtenue est appelée plasma quarks-gluons. Selon la théorie du «Big bang», un tel plasma quarks-gluons a pu exister durant les premières micro-secondes d'existence de l'Univers.
Complément : Quelques vidéos sur les plasmas
Une vidéo de l'ESPCI : "Plasma : à la rencontre du 4ème état de la matière"
Canal U : "Plasma : à la rencontre du 4ème état de la matière"
Une autre vidéo sur le 4ème état de la matière :
Définition : Modèle de plasma
Dans la suite, on choisit un modèle de plasma constitué de
ions (de masse
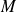et charge
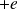) et de
électrons (de masse
et de charge
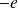) par unité de volume.
On néglige toutes interactions entre les ions : ni attraction ou répulsion électrostatique, ni chocs. Cette hypothèse est satisfaisante pour un plasma peu dense.
L'ionosphère est la partie de la haute atmosphère (75 à 250 km d'altitude en plusieurs couches) où les gaz sont ionisés par le rayonnement cosmique et par le vent solaire : c'est un exemple de tel plasma.
On note
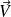et
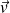les vitesses mésoscopiques d'un ion et d'un électron.
Si un champ électrique extérieur est appliqué au plasma :
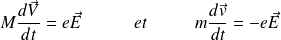
Par conséquent :
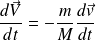
Soit, à une constante près :
Par conséquent, comme
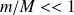, la vitesse des ions positifs est très faible vis-à-vis de celle des électrons.
On ne prendra en compte que le mouvement des électrons.
La densité volumique du plasma est :
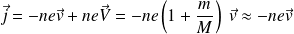
Elle est pratiquement égale à celle des électrons.
Méthode : Équations de Maxwell dans le plasma
On s'intéresse à la propagation d'une onde EM plane progressive monochromatique dans un plasma. On note
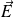et
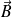les champs électrique et magnétique associés à cette onde.
Ces champs agissent sur les électrons du plasma et les mettent en mouvement.
L'équation du mouvement d'un électron est :
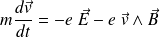
En admettant que (comme pour une onde dans le vide)
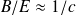, on voit que, tant que les ions ne sont pas relativistes :
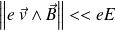
On pourra ainsi négliger la force magnétique vis-à-vis de la force électrique pour étudier le mouvement des électrons :
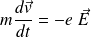
Les équations de Maxwell s'écrivent, en notant que la densité volumique de charges est nulle (le plasma reste globalement neutre) :
Avec :
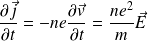
Fondamental : Équation de propagation et relation de dispersion des ondes électromagnétiques planes progressives monochromatiques
On utilise la relation d'analyse vectorielle afin de découpler les équations de Maxwell et obtenir l'équation de propagation vérifiée par le champ électrique
:
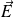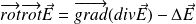
Soit :
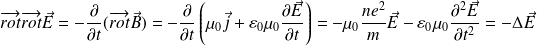
D'où :
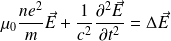
C'est l'équation de propagation vérifiée par le champ électrique
.
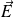On cherche une solution harmonique complexe de cette équation de propagation, sous la forme :
Il vient :
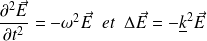
D'où :
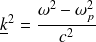
Avec :
(
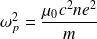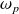est appelée pulsation plasma)
C'est la relation de dispersion de Klein-Gordon.
Deux cas sont alors à considérer :
Si
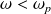, alors
est imaginaire pur : 
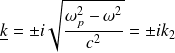
Le champ électrique de l'onde s'écrit alors sous la forme :
On obtient une onde stationnaire dite évanescente (évolution exponentielle de l'amplitude selon la direction de l'onde).
Si
,
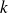est réel et vaut :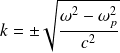 
Il y a propagation sans absorption.
Le plasma agit vis-à-vis des ondes EM comme un filtre passe-haut de pulsation de coupure
.
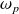Fondamental : Vitesse de phase et vitesse de groupe
On se place dans le cas où il y a propagation (soit
) :
L'onde se propage dans le sens des
, soit :
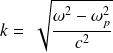
La relation entre
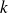et
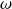est non linéaire : le milieu est dispersif.
Pour une onde réelle, qui est la superposition d'ondes planes progressives monochromatiques se propageant dans un milieu quelconque, il est possible de définir deux vitesses : la vitesse de phase et la vitesse de groupe.
La vitesse de phase est :
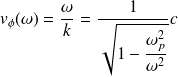
On remarque que
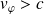; ceci n'est pas paradoxal car cette vitesse ne correspond pas à la vitesse de l'information ou de l'énergie (c'est le cas de la vitesse de groupe).
La vitesse de groupe est définie par :
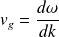
C'est la vitesse de propagation de l'enveloppe de l'onde (voir la fiche de cours sur la vitesse de groupe).
On montre qu'elle s'identifie généralement à la vitesse de propagation de l'énergie (ou de l'information).
Le principe de relativité impose que la vitesse de groupe est inférieure à la vitesse de la lumière dans le vide.
Pour la calculer, on peut différentier la relation de dispersion écrite sous la forme :
Soit :
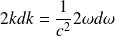
D'où :
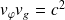
Et ainsi :
On remarque bien que
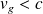.La vitesse de groupe dépend effectivement de
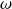, alors la phase de chaque onde plane progressive sinusoïdale se propage à sa propre vitesse. Une onde physique réelle, composée d'ondes planes progressives sinusoïdales, va se déformer au cours de sa propagation : c'est ce qu'on appelle la dispersion.
Méthode : Structure de l'onde plane progressive harmonique
Les équations de Maxwell :
,
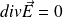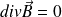et
Donnent, en notation complexe :
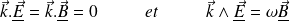
En notation réelle :
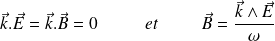
Le trièdre
est direct et :
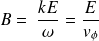
La structure de l'onde plane progressive monochromatique est semblable à celle du vide (seule la vitesse de phase est différente et dépend de la pulsation de l'onde).
Exemple : Quelques ordres de grandeur
L'ionosphère est la partie de la haute atmosphère (75 à 250 km d'altitude en plusieurs couches) où les gaz sont ionisés par le rayonnement cosmique et par le vent solaire.
La densité particulaire des électrons dans l'ionosphère est de l'ordre de
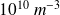à
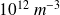et la fréquence plasma de l'ordre de
.
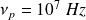Pour
, l'ionosphère joue le rôle de réflecteur : ceci explique la 1ère liaison radio transatlantique réalisée par Marconi en 1901. Ainsi des ondes radio en modulation d'amplitude peuvent atteindre des points très éloignés sur le globe.
Pour
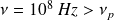, l'ionosphère est « transparente ». Ces fréquences sont utilisées pour communiquer avec les satellites.
Autre exemple : France inter GO et France Info FM
France Inter GO a pour fréquence
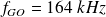et France info FM
.
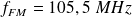On voit que
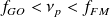: ainsi, les GO se réfléchissent sur l'ionosphère et pourront être captées à des distances nettement plus importantes du lieu d'émission que France Info dont les ondes se propagent dans l'ionosphère.
Complément : Pour aller plus loin ...
"Propagation des ondes radioélectriques à travers l'atmosphère" :
Propagation à travers la troposphère
Propagation à travers l'ionosphère
Par Laurent Castanet et Patrick Lassudrie-Duchesne.
