Ondes EM dans les métaux, effet de peau
Rappel : Courant de déplacement dans un conducteur ohmique
L'équation de Maxwell-Ampère s'écrit, compte tenu de la loi d'Ohm locale :
On note T le temps d'évolution caractéristique de la distribution (D) (sa période d'évolution).
On peut comparer le courant de conduction avec le courant de déplacement :
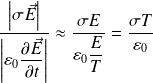
Pour le cuivre de conductivité :
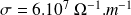
Ce rapport est de l'ordre de
, avec
en
.
Ainsi, même si T est de l'ordre de
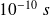(soit une fréquence de
) :
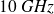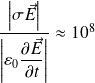
Par conséquent, pour les régimes d'évolution justifiant l'emploi de la loi d'Ohm, le courant de déplacement est, au sein du conducteur ohmique, négligeable devant le courant de conduction.
L'équation de Maxwell-Ampère s'écrit alors :
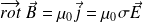
Rappel : Neutralité électrique
On suppose qu'à l'instant
, il existe en un point M intérieur au conducteur une charge volumique
.
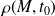Comment varie dans le temps cette charge volumique ?
L'équation de Maxwell-Gauss, la loi d'Ohm locale et la conservation de la charge électrique :
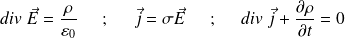
permettent d'écrire :
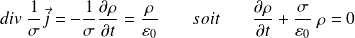
Par intégration :
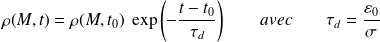
Pour le cuivre,
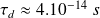: très rapidement, le conducteur devient neutre en volume :
Ainsi, comme en régime stationnaire, les charges s'accumulent au voisinage immédiat de la surface d'un conducteur, d'où l'intérêt de la notion de charge surfacique
.
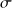Attention : Équations de Maxwell dans un conducteur
Finalement, dans le cadre de l'ARQS (Approximation des régimes quasi - stationnaires), le champ EM vérifie les équations de Maxwell « simplifiées » suivantes :
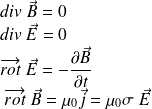
Ainsi, dans un conducteur, l'ARQS ne diffère des régimes stationnaires que par la prise en compte des phénomènes d'induction (équation de Maxwell-Faraday).
Complément : Loi des nœuds dans le cadre de l'ARQS
Puisque
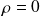, l'équation de conservation de la charge électrique conduit (à l'intérieur du conducteur) à :
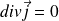
Le flux du vecteur courant volumique se conserve, entraînant ainsi la validité de la loi des branches et des nœuds dans le cadre de l'ARQS.
Remarque :
Il ne faut pas confondre
et
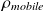: au sein du conducteur, qui reste globalement neutre,
.
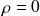Par contre, les porteurs de charges, dont la répartition de charges est
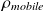, contribuent au vecteur densité de courant selon la relation :
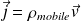
Attention : L'effet de peau
L'équation de propagation du champ électrique est :
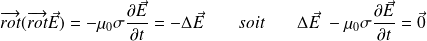
C'est une équation de type « diffusion », obtenue dans les transferts thermiques conductifs.
On cherche des solutions complexes de la forme :
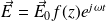
D'où :
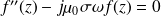
On pose :
Alors, en éliminant la solution qui diverge dans le métal (On suppose que l'axe Oz est orienté vers l'intérieur du métal de 0 vers l'infini) et en posant
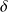l'épaisseur de peau :
On obtient :
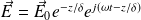
Le champ se propage dans le métal mais en étant atténué d'un facteur
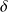, appelé épaisseur de peau :
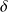correspond à l'ordre de grandeur de la longueur de pénétration de l'onde dans le métal.
Cette épaisseur sera d'autant plus faible que la conductivité du matériau et la fréquence de l'onde sont élevées.
L'onde est ici absorbée du fait de l'effet Joule au sein du conducteur, sur une épaisseur de l'ordre de quelques
.
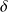Si l'on considère une onde EM de fréquence de l'ordre du GHz,
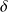est de l'ordre du
.
Cet effet de peau provoque la décroissance de la densité de courant à mesure que l'on s'éloigne de la périphérie du conducteur et conduit à une augmentation de la résistance du conducteur.
