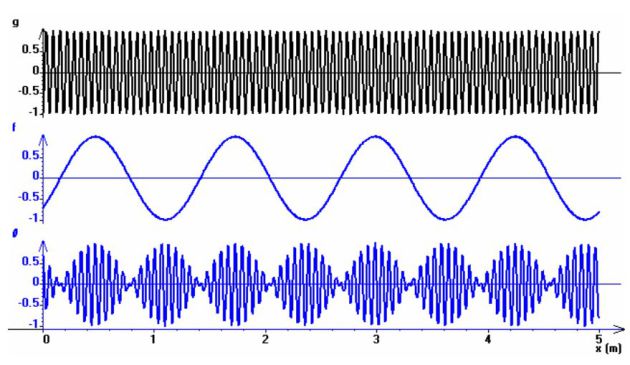
Vitesse de groupe d'un paquet d'ondes
Exemple : Propagation de deux ondes planes progressives harmoniques de fréquences voisines
On suppose que le vecteur d'onde est réel (on ne prend pas en compte l'absorption).
Soient
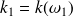et
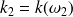les vecteurs d'onde réels des deux ondes.
On suppose que les pulsations
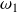et
sont proches et l'on pose :
Avec
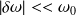et
.
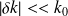On suppose de plus que les deux ondes ont même amplitude.
L'onde résultante, superposition de deux ondes, a pour amplitude :
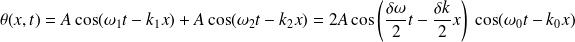
On observe des battements (figure du bas) : une onde moyenne de vecteur d'onde
est enveloppée par une onde enveloppe de vecteur d'onde
.
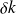Au cours du temps, l'onde moyenne (celle du haut sur la figure) constitue une onde plane progressive de vitesse
alors que l'onde enveloppe (celle du milieu) constitue une onde plane progressive de vitesse
.
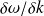Ces vitesses n'étant en général pas identiques, les crêtes de l'onde moyenne avancent à une vitesse différente de celle des crêtes de l'onde enveloppe.
Fondamental : Généralisation au cas d'un paquet d'ondes
On appelle paquet d'ondes un ensemble d'ondes planes progressives harmoniques de pulsations voisines.
Plus précisément, leurs pulsations sont comprises dans l'intervalle
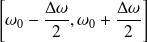, avec
.
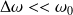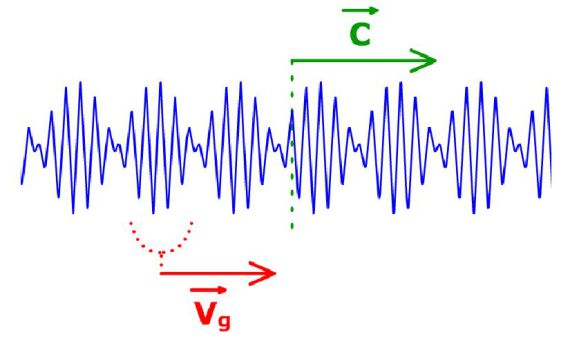
L'onde résultante peut s'écrire sous la forme d'une intégrale de Fourier :
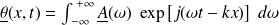
où l'amplitude
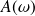ne prend de valeurs notables que sur l'intervalle
.
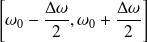En faisant un DVL au 1er ordre :
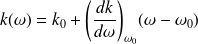
Il vient, en remplaçant
:
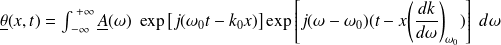
Soit :
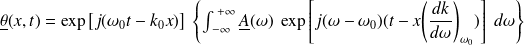
On pose :
Alors :
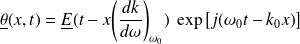
On voit ainsi apparaître une onde moyenne
de pulsation
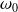se propageant à la vitesse de phase :
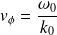
et une onde enveloppe
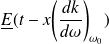qui ne dépend que de la variable :
et qui se propage à la vitesse dite de groupe :
Les vitesses de phase et de groupe sont a priori différentes et le paquet d'ondes se propage en se déformant.
En effet, chacune des composantes monochromatiques du groupe « chemine » avec sa propre vitesse, de telle sorte qu'on observe une déformation du paquet d'ondes tout au long de sa propagation.
On conçoit aussi que cette déformation est accompagnée d'un étalement du paquet d'ondes dû à l'avance croissante prise par les composantes de forte vitesse.
Complément : Une vidéo sur la signification de la vitesse de groupe
Attention : Vitesse de phase et vitesse de groupe
Pour une onde réelle, qui est la superposition d'ondes planes progressives monochromatiques se propageant dans un milieu quelconque, il est possible de définir deux vitesses :
La vitesse de phase :
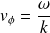
Elle correspond à la vitesse de propagation de la phase d'une composante monochromatique.
Elle n'a aucune réalité physique, c'est-à-dire ne correspond pas à un transport d'énergie.
La vitesse de groupe :
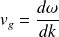
C'est la vitesse de propagation de l'enveloppe de l'onde.
On montre qu'elle s'identifie généralement à la vitesse de propagation de l'énergie (ou de l'information).
Le principe de relativité impose que la vitesse de groupe est inférieure à la vitesse de la lumière dans le vide.
Si
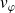dépend effectivement de
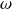, alors la phase de chaque onde plane progressive sinusoïdale se propage à sa propre vitesse.
Une onde physique réelle, composée d'ondes planes progressives sinusoïdales, va se déformer au cours de sa propagation : c'est ce qu'on appelle la dispersion.
