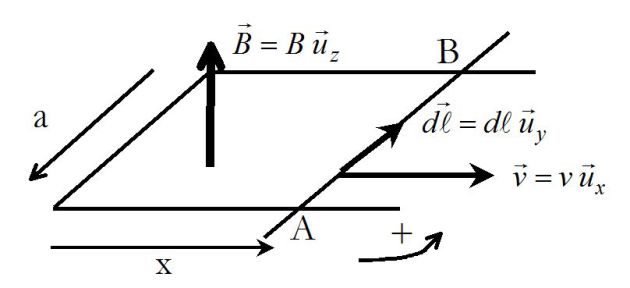
Rail de Laplace
La barre (AB), de longueur
et de masse
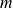, de centre de masse d'abscisse
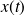et de vitesse
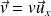(avec
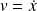) est lancée avec une vitesse initiale
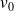sur des rails métalliques sur lesquels elle glisse sans frottement.
Elle constitue avec les rails de résistance négligeable un circuit rectangulaire (C) de résistance
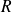constante et d'inductance négligeable et dont la surface à l'instant t est
.
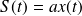Ce circuit est placé dans un champ magnétique permanent
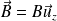d'origine extérieure à (C).
On souhaite déterminer la fém induite et la loi de vitesse de la barre.
Détermination de la fém induite
On utilise la loi de Faraday.
Pendant l'intervalle de temps dt, la variation du flux magnétique est :
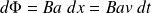
La fém induite vaut donc :
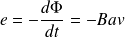
Le circuit peut alors être modélisé par :
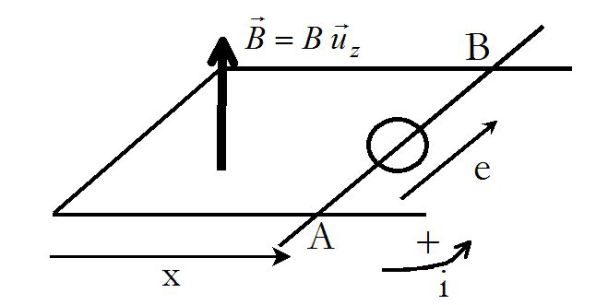
L'intensité qui traverse le circuit se calcule par la loi de Pouillet :
(C'est l'équation électrique (E))
Ainsi, pour
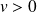, on en tire
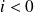: ce résultat pouvait être prévu à l'aide de la loi de Lenz.
En effet, lorsque la tige se déplace vers la droite, le flux inducteur (positif) augmente.
Par conséquent, le flux induit doit être négatif, ce qui correspond bien à un courant induit dans le sens négatif.
Loi de vitesse v(t)
La barre est soumise (horizontalement du moins) à la force de Laplace :
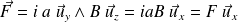
Ainsi, pour
,
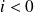: ce résultat peut là encore être prévu par la loi de Lenz.
En effet, l'apparition d'une force de freinage négative est bien un effet modérateur tendant à s'opposer à la mise en mouvement de la barre.
Le théorème du CI appliqué à la barre donne enfin : (c'est l'équation mécanique (M))
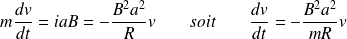
On peut remarquer que le terme
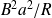joue le même rôle qu'un coefficient de frottement fluide.
On pose :
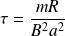
Le temps caractéristique du régime transitoire, alors :
Application numérique : a = 10 cm, B = 0,1 T, m = 10 g et R = 0,1 Ω. Alors
= 10 s.
Aspect énergétique (exemple de transducteur)
On reprend l'équation électrique (E) et l'équation mécanique (M) du circuit :
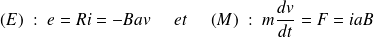
Afin de faire intervenir des puissances, on multiplie l'équation (E) par
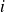et l'équation (M) par
:
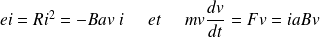
On note :
l'énergie cinétique de la barre ; alors :
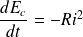
L'énergie cinétique perdue par la barre se retrouve intégralement sous forme d'effet Joule dans la résistance : la barre joue le rôle de convertisseur d'énergie mécanique en énergie électrique finalement dissipée par effet Joule en chaleur.
On peut également envisager le cas où la barre est initialement fixe et où l'introduction le long du circuit d'une source de tension (une pile par exemple) engendre un courant.
La barre se met alors en mouvement sous l'action des forces de Laplace et le même système joue le rôle de récepteur en convertissant cette fois de l'énergie électrique en énergie mécanique ; on a en fait le principe d'un moteur électrique.
D'une manière générale, on appelle « transducteur électromécanique » un système qui est susceptible de transformer l'énergie mécanique en énergie électrique et réciproquement.
Complément : Application de la loi de Lenz aux courants de Foucault
Selon un principe analogue à celui du montage précédent, les courants de Foucault induits dans les conducteurs massifs mobiles dans des champs magnétiques permanents sont à l'origine de forces de Laplace qui tendent à s'opposer au mouvement qui leur donne naissance.
Tel est le principe du freinage électromagnétique, utilisé notamment pour les poids lourds et les TGV.
