Inductance propre, inductance mutuelle
Inductance propre
Un circuit fermé filiforme (C) est parcouru par un courant d'intensité I.
Son champ magnétique propre
, donné par la loi de Biot et Savart, est proportionnel à I.
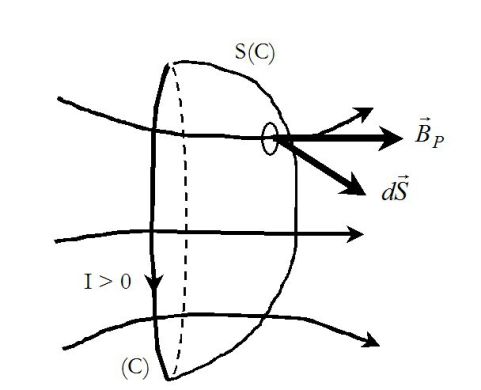
Le flux du champ magnétique propre à travers le contour orienté par le sens positif du courant choisi ou « flux propre » est proportionnel à I :
Le coefficient L ne dépend que des caractéristiques géométriques du circuit et s'appelle coefficient d'auto-induction ou d'inductance propre du circuit (C).
Signe de L :
Si
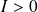, le champ magnétique a le sens représenté sur la figure et le flux est donc positif, donc
.
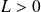De même, si
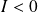, le champ magnétique change de sens et le flux devient négatif.
Par conséquent, L est un coefficient positif.
Le flux est exprimé en Weber et le coefficient L en Henry.
Attention : Définition de l'inductance propre d'un circuit filiforme
Exemple : Inductance propre d'un solénoïde
Le champ magnétique à l'intérieur du solénoïde « infini » est :
Le flux propre à travers N spires occupant une longueur
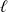est :
D'où l'inductance propre :
Ordre de grandeur :
Pour une bobine de longueur 10 cm comportant 100 spires dont le diamètre est de 1 cm, l'inductance propre est de l'ordre de 0,01 mH : le henry est une assez grande unité.
Des inductances propres plus importantes s'obtiennent avec une bobine à noyau de fer.
Mais la relation donnant L est plus compliquée (L dépend non seulement de la géométrie du circuit mais aussi de l'intensité).
Exemple : Inductance propre d'une bobine torique de section rectangulaire
On considère une bobine torique de section rectangulaire de hauteur h et de rayons a et b comportant N spires jointives parcourues par un courant I.
Un plan méridien est plan de symétrie ; en un point de ce plan, en cordonnées cylindriques, le champ propre est orthoradial et dépend a priori de r et de z :
Les lignes de champs sont des cercles d'axe (Oz).
On applique le théorème d'Ampère à la ligne de champ de rayon r :
Le champ ne dépend finalement pas de la cote z.
Le flux propre à travers les N spires vaut alors :
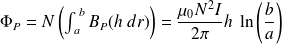
On en déduit l'inductance :
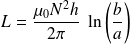
Inductance mutuelle
Deux circuits filiformes (C1) et (C2) sont parcourus par des courants d'intensités I1 et I2.
Le flux du champ magnétique
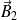à travers le contour fermé (C1) orienté par le sens positif du courant I1 est proportionnel à I2 :
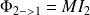
De même, le flux du champ magnétique
à travers le contour fermé (C2) orienté par le sens positif du courant I2 est proportionnel à I1 :
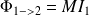
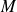est l'inductance mutuelle (ou coefficient d'induction mutuelle) des deux circuits.
Contrairement à l'inductance qui est toujours positive,
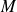est positive ou négative (selon l'orientation des circuits).
Remarque :
Si on sait calculer
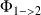, on en déduit
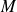et
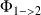. Parfois, le calcul de l'un des deux flux est compliqué alors que le calcul de l'autre est plus simple
