Loi de Lenz
Attention : Énoncé de la loi de Lenz
Le signe moins de la loi de Faraday résulte des conventions utilisées pour orienter la surface du circuit et définir la fém algébrique et, physiquement, de l'effet modérateur du courant induit.
La loi de Lenz traduit qualitativement cet effet.
Elle permet de prévoir le sens du courant induit dans les cas simples et de vérifier son signe une fois le calcul algébrique effectué.
Énoncé de la loi de Lenz :
« Le courant induit a un sens tel que le flux induit qu'il crée s'oppose aux variations du flux inducteur. »
ou encore :
« La fém induite tend par ses conséquences à s'opposer à la cause qui lui a donné naissance. »
Exemple : Vérification de la loi de Lenz sur un exemple
La variation du champ magnétique
dans le temps est cause d'un flux magnétique variable à travers le circuit, appelé « flux inducteur » et d'une fém induite qui peut débiter un courant dans le circuit (appelé « courant induit »).
Le courant induit créé un champ magnétique propre
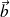ou « champ magnétique induit » responsable d'un flux magnétique à travers le circuit appelé « flux induit ».
Si le flux inducteur augmente (la norme du champ
augmente), sa dérivée est positive et d'après la loi de Faraday, la fém induite est négative.
Le courant induit est alors négatif.
Le champ induit
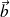s'en déduit (règle de Biot et Savart ou du tire-bouchon) et le flux induit est donc négatif quand la variation du flux inducteur est positive : le flux induit s'oppose donc à la variation du flux inducteur, ce qui illustre, sur cet exemple, la loi de Lenz qui apparaît bien comme une loi de modération.
Complément : Courant de Foucault
Simulation : Animation JAVA de JJ.Rousseau (Université du Mans)
Loi de Lenz : cliquer ICI
