Un MOOC pour la Physique

On considère un porteur de charge plongé dans un champ magnétique indépendant du temps et se déplaçant à la vitesse 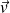par rapport au conducteur, lui-même se déplaçant à la vitesse 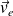par rapport au référentiel du laboratoire (R₀).

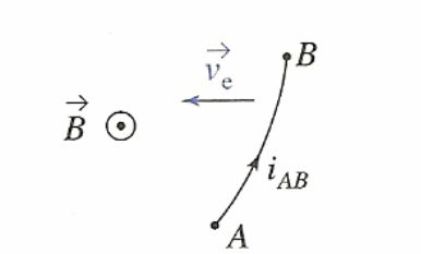
Dans ce référentiel, le porteur de charge a une vitesse ( 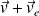) et subit la force de Lorentz

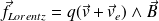
dont la puissance est nulle :

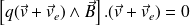
Cette puissance peut être décomposée en 4 termes dont deux sont nuls :

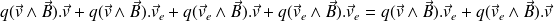
Dans un volume élémentaire 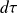, le nombre de porteurs de charge est 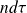et la puissance volumique de la force de Lorentz devient :

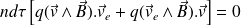
Le terme 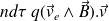représente la puissance volumique de la force appliquée aux charges due au champ électromoteur 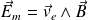évaluée dans le référentiel du conducteur ; en sommant sur tout le volume du conducteur, on obtient la puissance de la fém induite, notée :

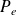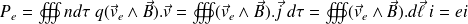
Interprétation du terme  :

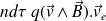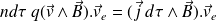
Ce terme apparaît comme la puissance de la force de Laplace subie par l'élément de volume .

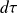Finalement, par intégration :

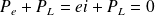
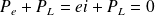
La puissance de la force électromotrice d'induction est compensée par celle des actions de Laplace exercées sur le circuit.