Équation locale de conservation de la charge
Rappel :
On considère un volume V délimité par une surface fermée S (fixe dans le référentiel d'étude). Soit ρ la densité volumique de charges mobiles dans le milieu.
La charge totale Q(t) comprise dans le volume à l'instant t vaut :
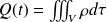

La conservation de la charge électrique permet d'écrire :
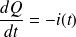
Par conséquent :
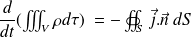
Le volume (V) étant fixe :

Finalement, le principe de conservation de la charge conduit à :
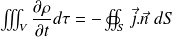
En utilisant le théorème de Green-Ostrogradsky :
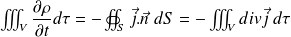
Soit :
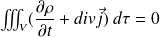
Ce résultat étant vrai pour tout volume (V), il vient :
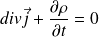
C'est l'équation locale de conservation de la charge électrique.
Attention : Équation locale de conservation de la charge
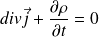
Remarque : Bilan local de conservation
Une telle forme d'équation se retrouve couramment lorsque l'on fait le bilan d'une grandeur scalaire extensive qui, en l'absence de sources, obéit à un principe de conservation :
Conservation de l'énergie EM (vecteur de Poynting)
Conservation de la masse (en mécanique des fluides)
Équations de la diffusion et de la chaleur (phénomènes de transport).





