Contenus physiques des équations de Maxwell
Rappel :
Les équations « locales » de Maxwell donnent, par intégration, des lois et théorèmes connus qui peuvent être vérifiés expérimentalement.
Équation de Maxwell-Gauss et théorème de Gauss :
On part de l'équation de Maxwell-Gauss, , afin de calculer le flux sortant du champ électrique à travers une surface fermée (S) :
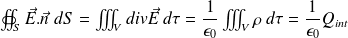
où Qint désigne les charges intérieures à la surface fermée (S).
Le théorème de Gauss apparaît ainsi encore valable en régime dépendant du temps, même si les charges électriques peuvent être en mouvement.
En régime permanent, les sources du champ électrique sont les charges caractérisées par la densité ρ. Les lignes de champ divergent à partir des charges positives à la manière d'un fluide sortant d'une véritable source et disparaissent sur les charges négatives comme un fluide dans un puits.
Tel est encore le cas en régime non permanent, à la différence près que (voir conséquence de l'équation de Maxwell-Faraday), ρ n'est plus la seule source du champ électrique, de telle sorte que les cartes de champ électrique n'ont plus nécessairement la même allure.
Équation de Maxwell-Ampère et théorème d'Ampère :
On calcule la circulation à un instant donné du champ magnétique le long d'un contour (C) sur lequel s'appuie une surface (S) et on utilise l'équation de MA :
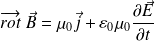
Il vient :
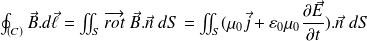
On reconnaît :
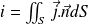
l'intensité qui traverse (S).
On peut noter que, en régime non permanent, cette grandeur ne dépend pas seulement de (C) mais de la surface (S) car
n'est plus à flux conservatif.Alors : (théorème d'Ampère généralisé)
Où le terme :
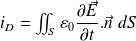
s'interprète comme le flux du courant de déplacement à travers la surface (S).
Ainsi, en régime non permanent, les sources du champ magnétique sont de deux natures : les courants « réels » et le courant de déplacement qui provient de la dépendance temporelle du champ électrique.
En régime permanent, on retrouve bien évidemment le théorème d'Ampère classique :
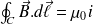
Équation du flux magnétique et champ magnétique à flux conservatif :
L'équation locale
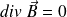permet de montrer que :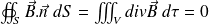
Ainsi :
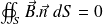
Le champ magnétique est à flux conservatif. Par conséquent :
Le flux magnétique se conserve à chaque instant à travers toute section d'un tube de champ magnétique
Il est possible de définir le flux magnétique qui traverse un contour (C) sans avoir à préciser la surface (S) qui s'appuie sur celui-ci
En comparant avec l'expression du théorème de Gauss, on constate que le champ magnétique n'a pas de sources qui joueraient pour B le rôle que les charges jouent pour E. Autrement dit, il n'existe pas de charges magnétiques (de monopôles magnétiques).
Équation de Maxwell-Faraday et loi de Faraday :
On évalue la circulation e du champ électrique le long d'un contour (C) fermé sur lequel s'appuie une surface (S) et on utilise l'équation de Maxwell-Faraday :
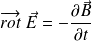
Sous la forme :
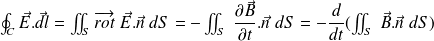
On note :
la force électromotrice induite sur le contour (C) et :
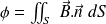
le flux du champ magnétique à travers une surface s'appuyant sur le contour. On a alors :
C'est la loi de Faraday qui régit les phénomènes d'induction électromagnétique, dégagée expérimentalement par Faraday en 1831.
La circulation du champ E n'est plus nulle : un champ magnétique variable dans le temps est source d'un champ électrique à circulation non conservative.
Attention : Contenus physiques des équations de Maxwell
Théorème de Gauss :
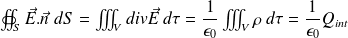
Théorème d'Ampère "généralisé" :
Le champ magnétique
est à flux conservatif :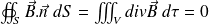
Loi de Faraday :
