Bilan d'énergie électromagnétique
Rappel : Puissance volumique cédée par le champ EM à la matière
Un champ EM va interagir avec des particules chargées et leur fournir de l'énergie.
En effet, une charge q est soumise de la part de ce champ EM à la force de Lorentz, dont la puissance s'écrit :
En notant n le nombre de porteurs de charges par unité de volume, la puissance volumique cédée par le champ EM à la matière s'écrit donc :
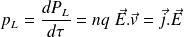
Remarque :
La puissance reçue par le champ EM de la part des porteurs de charge est
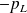(faire l'analogie avec
, puissance volumique reçue par un milieu conducteur de la chaleur de la part des sources de chaleur).
Rappel : Équation de conservation de l'énergie lors des phénomènes conductifs (voir cours sur les transferts thermiques)
On considère un volume V délimité par une surface fermée S (fixe dans le référentiel d'étude).
L'énergie interne totale U(t) comprise dans le volume à l'instant t vaut :
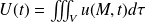
Où
est l'énergie interne volumique.
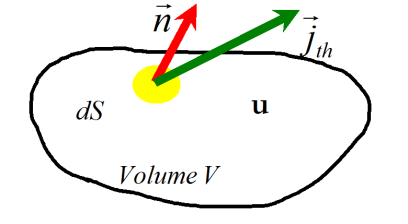
La conservation de l'énergie interne permet d'écrire :
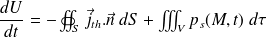
Le volume (V) étant fixe :
En utilisant le théorème de Green-Ostrogradsky, il vient :
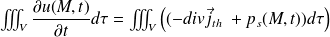
Ce résultat étant vrai pour tout volume (V), il vient :
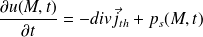
Cette équation avait été démontrée dans le cas à une dimension.
Équation locale de conservation de l'énergie EM
Par analogie avec les équations de conservation (charge, masse, diffusion, chaleur), on souhaite obtenir une équation du type :
Où
désigne l'énergie électromagnétique volumique (contenue dans le champ EM) et
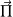un vecteur (appelé vecteur de Poynting) sensé donner le sens des échanges d'énergie EM (notamment par le calcul de son flux à travers une surface).
Le calcul suivant n'est pas au programme des CPGE :
On exprime le produit
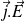en utilisant l'équation de Maxwell-Ampère :
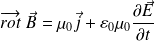
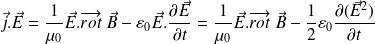
En écrivant que :
Soit :
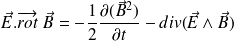
Il vient :
D'où :
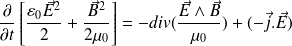
On est ainsi amené à poser :
Densité volumique d'énergie électromagnétique :
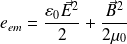
Vecteur de Poynting :
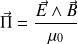
Cette équation se réécrit alors :
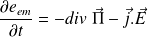
et correspond bien alors à un bilan d'énergie EM.
Attention : Bilan d'énergie de Poynting
Densité volumique d'énergie électromagnétique :
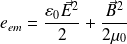
Vecteur de Poynting :
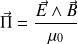
Bilan local de conservation de l'énergie EM :
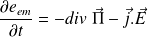
La forme intégrale de la conservation de l'énergie EM est :
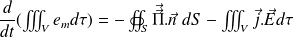
Remarque : Vitesse de propagation de l'énergie
Par analogie avec l'équation de conservation de la charge, on peut définir la vitesse de propagation de l'énergie (notée
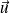) par la relation :
Exemple : Bilan énergétique pour un fil conducteur ohmique
On considère un fil conducteur ohmique de conductivité
, assimilé à un cylindre d'axe (Oz) et de rayon a, soumis au champ électrique uniforme et permanent (à l'intérieur et à l'extérieur du fil) :
Le fil est alors parcouru par des courants de densité uniforme :
Le champ magnétique créé par cette distribution est de la forme :
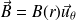
Et se calcule en écrivant le théorème d'Ampère.
On obtient (en notant
l e courant total qui traverse une section transverse du fil) :
Pour
: 
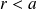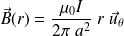
Pour
: 
Le vecteur de Poynting vaut :
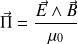
Ainsi :
Pour
: 
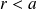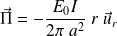
Pour
: 
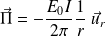
On rappelle l'expression générale de conservation de l'énergie EM :
Dans ce cas particulier (régime stationnaire) :
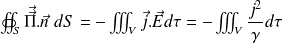
Physiquement, la puissance dissipée par effet Joule est évacuée en dehors du volume (V) en régime stationnaire.
On calcule le flux sortant du vecteur de Poynting à travers un cylindre d'axe (Oz) et de rayon r.
Pour
: 
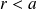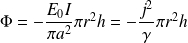
Pour
: 
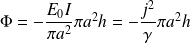
On reconnaît bien, dans les deux cas, la puissance absorbée par effet Joule dans le cylindre de rayon r considéré et on vérifie bien l'équation de conservation précédente.
