Onde de température
(15 minutes de préparation)
Le sous-sol est considéré comme un milieu semi-infini, homogène, de conductivité thermique K, de masse volumique ρ, de capacité thermique massique c, situé dans le demi-espace x > 0. On suppose que la température de la surface du sol (plan x = 0) est soumise à des variations sinusoïdales :

Question
Déterminer la température T(x,t) à la profondeur x (se placer en notation complexe) en régime permanent.
Résoudre l'équation de la chaleur en utilisant la méthode complexe.
Cet exercice traite l'équivalent de l'effet de peau en électromagnétisme.
L'équation de la chaleur s'écrit :
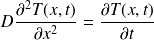
On utilise la méthode complexe et on pose :
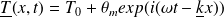
L'équation de la chaleur donne alors :
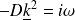
Soit encore :
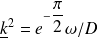
Par conséquent :

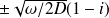
On pose : (épaisseur de peau)
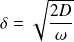
En repassant en notation réelle et en ne gardant que la solution qui ne diverge pas en l'infini :
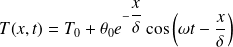
Question
Exprimer la vitesse v de l'onde thermique ainsi obtenue.
La vitesse de l'onde thermique est :

Question
On considère des variations journalières de la température, la température au niveau du sol variant entre 0°C la nuit et 16°C le jour.
A partir de quelle profondeur les variations de température sont-elles inférieures à 1°C ? Calculer la vitesse v. On donne

On considère des variations annuelles de température, la température variant de – 10°C à 26°C. Répondre aux mêmes questions.
1er cas : x = 26,7 cm et v = 80,7 cm.s–1.
2ème cas : x = 7,1 m et v = 4,2 cms.s-1 : ainsi, la température d'une cave enterrée paraît fraîche l'été et douce l'hiver. En effet, à une profondeur de 4,2 m, l'évolution de la température reflète celle de l'extérieur avec un retard de 100 jours.





