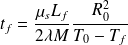Fonte d'un glaçon
(15 minutes de préparation)
Un glaçon sphérique, de centre fixe O, de rayon initial R0 est immergée dans de l'eau liquide et fond lentement.
On note respectivement λ la conductivité thermique du liquide, ρs et c la masse volumique et la capacité calorifique massique du solide, Lf et M l'enthalpie molaire de fusion et la masse molaire de l'eau.
On suppose la conductivité thermique du solide infinie, ce qui lui permet d'avoir à chaque instant une température uniforme, et la capacité calorifique massique du liquide négligeable.
Au cours de la fusion, le glaçon reste sphérique (on note R(t) son rayon à l'instant t) à la température de fusion Tf et, loin du solide, le liquide conserve une température constante T0 > Tf. Il n'y a pas de convection.
Question
Déterminer la température T(r,t) dans le liquide en fonction de r et de R(t).
L'équation de la chaleur s'écrit ici :
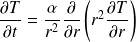
Avec :

La capacité calorifique du liquide étant négligée, α tend vers l'infini. Par conséquent :
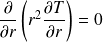
D'où :
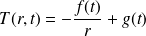
Les conditions aux limites donnent :
 et
et
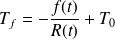
On en déduit :
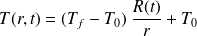
Question
Effectuer un bilan d'énergie pour le glaçon entre les instants t et t + dt et en déduire l'équation différentielle vérifiée par R(t).
Le vecteur densité de courant thermique vaut :
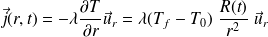
Pendant dt, le glaçon reçoit de la part du fluide la quantité de chaleur :
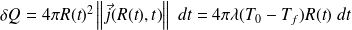
Cette quantité de chaleur permet de faire fondre une masse dm > 0 de glace telle que :
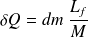
Or :
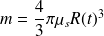
Donc :
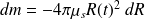
D'où :
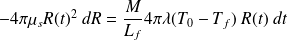
Finalement :

Question
Déterminer R(t) et exprimer la durée nécessaire tf à la fusion complète du glaçon.
On en déduit :
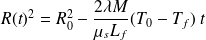
Et :