Évaporation
(15 minutes de préparation)
Une soucoupe de rayon R = 5 cm et de hauteur L = 2 cm contient de l'eau sur une hauteur h = 3 mm.
Elle est placée dans une pièce à T = 298 K, l'ensemble est initialement à cette température.
On donne :
Coefficient de diffusion de l'eau dans l'air à 25 °C, D≈ 2. 10-5 m2.s-1
Pression de vapeur saturante de l'eau à 25°C : Ps ≈ 3200 Pa.
Question
Au bout de combien de temps n'y a-t-il plus d'eau dans la soucoupe ?
Penser à se placer dans l'ARQS et à utiliser les conditions aux limites.
Soit Oz l'axe vertical orienté vers le haut ; on suppose que la diffusion de fait selon cet axe. Les conditions aux limites sont :
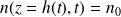
où n0 est donnée par la valeur de la pression de vapeur saturante, soit :
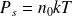
Et :
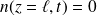
En considérant que la vapeur d'eau est emportée par l'air.
On se place dans l'ARQS :
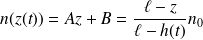
Le vecteur densité de particules vaut ensuite :
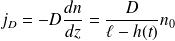
Or :
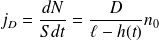
D'où :
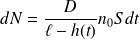
Ces particules qui diffusent pendant dt proviennent du volume Sdh d'eau liquide qui va se vaporiser, par conséquent :
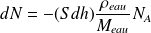
D'où :
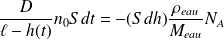
Soit :
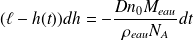
En intégrant entre t = 0 (alors h(0) = h0) et h(tf) = 0 :






