Approche probabiliste de la diffusion
(15 minutes de préparation)
Dans un tube cylindrique compris entre x = -L/2 et x = L/2, des neutrons sont répartis à un instant
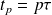avec p entier sur des sites discrets d'abscisses xp = na avec n entier.
Entre les instants tp et tp + 1 , chaque neutron a une probabilité
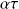de disparaître.
S'il ne disparaît pas, il a une même probabilité d'effectuer un saut vers l'un ou l'autre des deux sites voisins situés à sa gauche et à sa droite.
Question
On note p(xn, tp) la probabilité pour un neutron donné d'être en xn à l'instant tp. Exprimer p(xn , tp) en fonction de p(xn - 1, tp) et de p(xn + 1, tp).
Question
On fait l'approximation des milieux continus. Montrer que p(x, t) est solution d'une équation aux dérivées partielles de la forme :
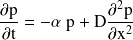
et exprimer D en fonction des données. Vérifier son homogénéité. De quelle équation aux dérivées partielles est solution la densité linéique n(x, t) de neutrons ?
Question
On suppose que le matériau reçoit en x = ± L/2 un flux stationnaire de neutrons. Déterminer n(x) en régime stationnaire.
