Diffusion d'un pic de concentration
(15 minutes de préparation)
Un tube de longueur L et de section S est suffisamment long suivant Ox et les temps d'étude suffisamment courts pour que l'on puisse négliger les effets de bord aux extrémités.
A l'origine des temps, les molécules étudiées sont très fortement concentrées dans le plan Oyz, soit N0 leur nombre. Elles diffusent dans un fluide support et leur coefficient de diffusion est D.
Question
A quelle condition sur la constante a la fonction :
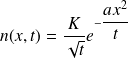
est-elle solution de l'équation de diffusion ?
L'équation de diffusion des molécules est :
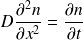
Avec :
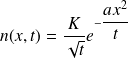
On calcule :
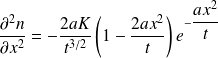
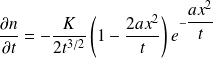
L'équation est vérifiée si :
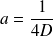
Question
Pour quelle valeur de la constante K satisfait-elle aux conditions initiales ?
Tracer l'allure de la courbe n(x,t) à deux instants t1 et t2 > t1.
Cette solution vérifie :
La condition initiale
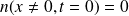car en t=0, toutes les molécules sont en x=0.Les conditions aux limites
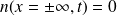, car la diffusion n'atteint pas les extrémités du tube.
Il reste à traduire la conservation du nombre de molécules dans le tube de section S et de très grande longueur :
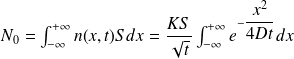
Le changement de variable :
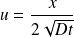
Conduit à :
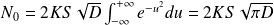
Ainsi :
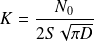
Et finalement :
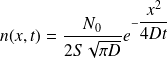
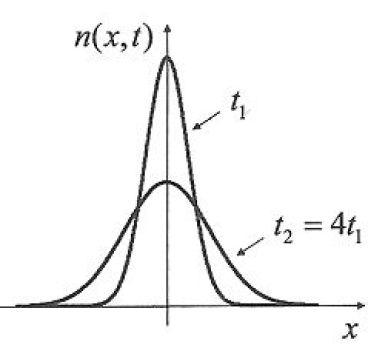
Au cours du temps, ce profil gaussien s'élargit en s'aplatissant, l'aire sous la courbe, liée aux nombre de molécules, étant constante.
Question
Donner la probabilité dP = p(x,t)dx pour une molécule d'être à l'instant t dans la tranche en x d'épaisseur dx et en déduire l'abscisse moyenne <x> et la distance quadratique moyenne xm.
On donne :
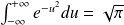et
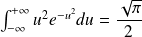
Si dN=n(x,t)Sdx est le nombre de molécules présentes à l'instant t dans la tranche d'épaisseur dx, la probabilité cherchée est :
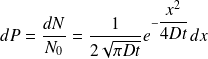
Alors :
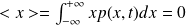
par intégration d'une fonction impaire sur un intervalle symétrique. La position moyenne des molécules (leur barycentre) reste en x=0 car la distribution est symétrique par rapport à ce plan.
La distance quadratique moyenne xm est telle que :
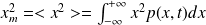
Soit :
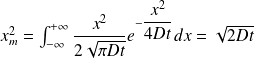
La distance quadratique moyenne croît comme la racine carrée du temps, c'est-à-dire qu'au cours du temps, la distance atteinte s'étend de moins en moins vite. On dit que la diffusion s'essouffle avec la distance, ce qui est un comportement caractéristique.
Question
En prenant pour un soluté dans l'eau D=2.10-9 m2.s-1, estimer le temps nécessaire pour que la diffusion atteigne une distance de 1 mm, puis 1 cm.
Pour xm=1 mm, il faut t de l'ordre de 4 min, alors que pour xm = 1 cm, il faut 7 h.
