La mécanique de la marche
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Par un beau matin printanier, un étudiant décide de se promener à travers la campagne.
Après 10 km de marche sur un chemin horizontal, il s'assoit à l'ombre d'un arbre et constate qu'il est fatigué alors qu'il n'a pourtant pas apparemment travaillé !
Comment est-ce possible ?
Question
L'étudiant, de masse M, effectue une marche de
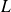kilomètres à vitesse constante sur une route horizontale.
On suppose que le centre d'inertie du promeneur conserve une altitude constante pendant la marche et que le contact sol-promeneur se fait sans glissement.
Quel est le travail mécanique effectué par l'étudiant lors de la marche, en assimilant celui-ci à un corps rigide ?
Le corps humain n'est pas un corps solide. Au cours de la marche, le centre d'inertie effectue des oscillations verticales.
L'ordre de grandeur de l'amplitude de ces oscillations est
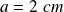pour chaque pas effectué.
Quand le centre d'inertie s'élève, l'énergie élastique musculaire est transformée en énergie potentielle. Quand le centre d'inertie s'abaisse, l'énergie potentielle est convertie en énergie thermique (chaleur).
La machine humaine n'est pas réversible.
Données :
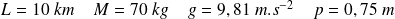(une longueur de pas)
On assimile l'étudiant à un corps rigide de masse M, dont le centre d'inertie conserve une altitude constante.
Par conséquent, le travail du poids est nul ainsi que le travail des forces intérieures à l'étudiant.
Par ailleurs, le contact étudiant-sol s'effectuant sans glissement, le travail de la réaction du sol sur l'étudiant est nul. Au bout du compte, l'étudiant n'effectue aucun travail mécanique.
Question
Montrer que cette marche est équivalente pour le travail fourni (par un étudiant de nouveau considéré comme un corps rigide) à l'escalade d'une montagne de hauteur H que l'on précisera.
La figure précise les notations.
Lorsque l'étudiant avance d'un pas, son centre d'inertie G de déplace, de manière irréversible, d'une hauteur égale à 4a.
Le nombre de pas réalisés par l'étudiant étant
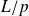, le travail du poids devient :
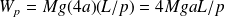
Ce travail est identique à celui fourni lors de la montée d'une montagne de hauteur H donnée par :
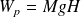
Soit une hauteur :
Question
Calculer l'énergie mécanique fournie et comparer cette énergie à l'énergie de la ration alimentaire quotidienne d'un homme sédentaire (environ 106 J). Que peut-on en conclure ?
L'énergie mécanique fournie lors de la marche vaut :
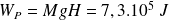
Soit pratiquement l'énergie de la ration alimentaire de l'étudiant sédentaire ; celui-ci peut effectivement se sentir fatigué.
Question
Pour marcher l'étudiant prend appui sur une jambe et laisse « penduler » l'autre jambe autour de l'articulation fémorale.
On modélise la jambe par une barre homogène, de masse m, de longueur
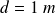, de moment d'inertie autour de l'articulation
.
Quelle est la période des petites oscillations ?
En déduire la vitesse moyenne du marcheur en
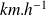. Quelles conséquences peut-on en tirer ?
On modélise la jambe par un pendule simple mobile autour du point O (articulation fémorale), de longueur d et de masse m.
Le moment du poids de la jambe par rapport à l'axe de rotation est :
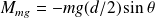
Le théorème du moment cinétique appliqué dans le référentiel galiléen lié au marcheur, par rapport à l'axe de rotation, s'écrit :
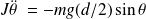
Si on se limite aux petites oscillations,
(
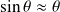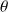en rad), alors, avec
:
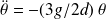
La période des petites oscillations de la jambe est alors :
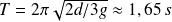
Un pas étant effectué en une demi-période, la vitesse moyenne de l'étudiant vaut :
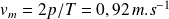
Soit environ :
Le modèle utilisé ici donne une vitesse de marche un peu faible ; on peut en effet penser que l'étudiant, jeune et sportif, arrive à marcher à une allure plus soutenue !
Question
Sachant que
sur la Lune, estimer la vitesse moyenne de l'étudiant sur la Lune.
Sur la Lune, où le champ de pesanteur vaut
, la période des oscillations de la jambe sera :
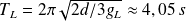
Et la vitesse moyenne :
