Chute d'une tartine beurrée
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On modélise une tartine beurrée par un parallélépipède de longueur 2a, de largeur b, d'épaisseur négligeable et de masse m uniformément répartie.
La tartine est placée au bord d'une table de hauteur h >> a.
Le mouvement est décrit dans le repère R(O,x,y,z) direct et supposé galiléen : O est sur le bord de la table, l'axe (Ox) est horizontal dirigé vers l'extérieur de la table, l'axe (Oy) est porté par le rebord de la table et l'axe (Oz), vertical, est dirigé vers le bas.
Les petits côtés de la tartine sont parallèles à (Oy).
A l'instant initial, la tartine est horizontale et sa vitesse nulle.
Les coordonnées de son centre d'inertie G sont (δ,0,0).
La tartine amorce une rotation sans glissement autour de l'arête (Oy) du bord de la table.
A l'instant t, la tartine est repérée par l'angle θ (voir figure, ). La vitesse angulaire est notée ω.
Le moment d'inertie de la tartine par rapport à l'axe (Gy), parallèle à (Oy) et passant par G vaut
.
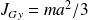Question
En admettant que la tartine constitue un système conservatif, montrer que, lors de la rotation autour de l'arête de la table :
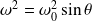
Avec :
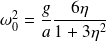et
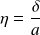
Cet exercice illustre le principe de Murphy, ou encore le principe de "l’emmerdement" maximal !
Alors, pas d'aide sur cet exercice !
La loi de Murphy est d'ailleurs vérifiable (ou applicable) dans toutes les situations.
La preuve : si votre tartine beurrée tombe du côté non beurré, c'est bien sûr parce que vous avez beurré le mauvais côté. N'est-ce pas le comble de la malchance ?
Le moment d'inertie de la tartine par rapport à l'axe (Oy) est, d'après le théorème de Huygens :
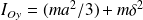
L'énergie cinétique est alors :
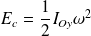soit
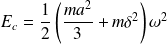
L'énergie potentielle de la tartine vaut :
soit
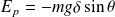
A l'instant initial :
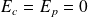
La conservation de l'énergie mécanique de la tartine (considérée ici comme étant un système conservatif) lors de la rotation autour de l'arête de la table donne :
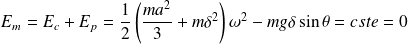
D'où l'expression donnée dans l'énoncé :
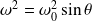
Avec :
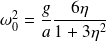et
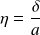
Question
La tartine quitte la table à un instant pris comme origine des temps, l'angle θ vaut alors π/2 et la vitesse angulaire initiale ω0.
Quelle est la loi d'évolution ultérieure de l'angle θ (on suppose que le mouvement de G reste plan et qu'il n'y a pas de contact ultérieur avec la table), en négligeant les frottements dus à l'air ?
Soit
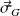le moment cinétique barycentrique de la tartine beurrée.
Le théorème du moment cinétique appliqué dans le référentiel barycentrique donne, puisque la tartine n'est soumise qu'à son poids de moment nul par rapport à G :
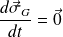soit
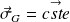
La règle du « tire-bouchon » permet d'écrire le vecteur vitesse angulaire sous la forme :
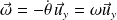
Alors :
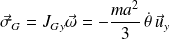
On en déduit finalement que
(avec
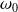choisie ici positive) : la vitesse angulaire de la tartine est constante.
La loi d'évolution de l'angle θ en fonction du temps lors de la chute de la tartine s'en déduit :
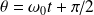
Question
Dans les circonstances courantes, le coefficient de surplomb
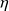ne dépasse guère 0,02.
On pourra donc supposer, dans la suite, que
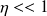(soit δ << a).
Exprimer alors la durée de chute
de la tartine en fonction de h et g.
Calculer
pour h = 75 cm et g = 9,8 m.s-2. Quelle est la chance de rattraper la tartine avant qu'elle n'atteigne le sol ?
Le théorème du centre d'inertie appliqué à la tartine donne :
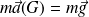soit
Pour
,
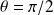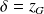et
. Par conséquent, en projection selon (Oz) :
considérant a << h, la tartine touche le sol pour
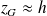, c'est-à-dire à l'instant
tel que :
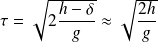
L'application numérique donne
= 0,39 s : la probabilité de rattraper la tartine avant qu'elle ne touche le sol semble bien faible !
Question
Déterminer l'angle θ1 dont a tourné la tartine lorsqu'elle heurte le sol. Faire l'application numérique avec
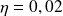et a = 5 cm. Conclusion.
Lorsque la tartine touche le sol, l'angle θ vaut :
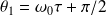
Numériquement, avec ω0 = 4,85 rad.s-1, θ1 = 3,46 rad = 200° : la tartine atterrit du côté beurré !
Complément : Corollaires et extensions à la loi de Murphy
Quelques phrases à méditer :
À la fin tout tourne mal ; si ça semble s'arranger, c'est que ce n'est pas encore la fin
Rien n'est aussi facile qu'il n'y paraît
Toute solution amène de nouveaux problèmes
Laissées à elles-mêmes, les choses ont tendance à évoluer de mal en pis
La loi des séries, qui postule qu'un événement désastreux doit en entraîner d'autres, similaires, à sa suite. On dit alors qu'« un ennui n'arrive jamais seul », ou encore « il y a des jours comme ça, où on ferait mieux de rester au lit ». (Jacques Chirac disait que « les emmerdes volent toujours en escadrille ».)
D'abord les ennuis s'additionnent, ensuite ils se multiplient
Le prix d'un ordinateur baisse de 50 % le lendemain de son achat. » Syndrome de l'Acheteur de la Veille
L'erreur est humaine, mais pour provoquer une vraie catastrophe, il faut un ordinateur
Ne pensez jamais que ça va marcher au moment où vous en aurez le plus besoin. » Règle de Base n°1 de l'Informatique
Le travail d'équipe est fondamental, ça donne à l'ennemi d'autres cibles que vous
Le travail d'équipe est essentiel. Ça donne quelqu'un d'autre sur qui rejeter la faute
Si l'ennemi est à votre portée de tir, vous êtes aussi à sa portée
La démocratie est le pire des régimes, à l'exception de tous les autres
Les politiciens sont là pour régler les problèmes que l'on n'aurait pas s'il n'y avait pas de politiciens
Mieux vaut avoir des ennemis que des amis, les ennemis eux au moins sont fidèles
La probabilité que quelque chose arrive est inversement proportionnelle à sa désirabilité
La probabilité de gagner au loto est légèrement plus élevée si vous achetez un ticket
Plus ça rate, plus on a de chance que ça marche
Les affaires triviales sont réglées rapidement, les affaires importantes ne sont jamais résolues
Les premiers 90 % d'une tâche prendront les 10 % du temps, et les derniers 10 % prendront les autres 90. » La loi des 90/90 de la planification d'une tâche.
La théorie c'est quand ça ne marche pas mais que l'on sait pourquoi. La pratique, c'est quand ça marche mais qu'on ne sait pas pourquoi. Quand la théorie rejoint la pratique, ça ne marche pas et on ne sait pas pourquoi
Vous ne retrouverez quelque chose qu'au dernier endroit où vous le chercherez
