Vidange d'une clepsydre
(20 minutes de préparation)
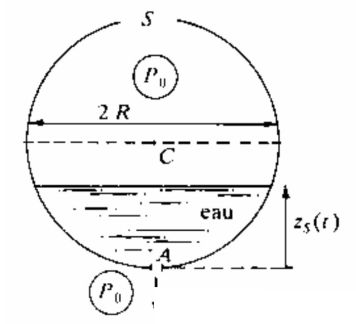
Un réservoir de forme sphérique, de rayon R = 40 cm, est initialement rempli à moitié d'eau de masse volumique ρ = 103 kg.m– 3.
La pression atmosphérique P0 règne au-dessus de la surface libre de l'eau grâce à une ouverture pratiquée au sommet S du réservoir.
On ouvre à t = 0 un orifice A circulaire de faible section s = 1 cm2 au fond du réservoir.
Question
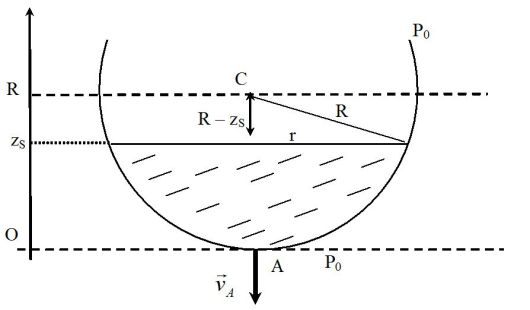
Établir l'équation différentielle en zs(t), si zs(t) est la hauteur d'eau dans le réservoir comptée à partir de A, à l'instant t.
En négligeant la vitesse de la surface libre de l'eau, le théorème de Bernoulli entre la surface et la sortie A donne :
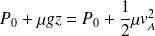
D'où :
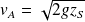
On retrouve la formule de Torricelli.
L'eau étant incompressible, le débit volumique se conserve :
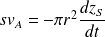
Or :
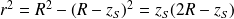
Soit, après avoir séparé les variables :
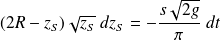
Question
Exprimer littéralement, puis calculer, la durée TS de vidange de ce réservoir.
La durée de vidange TS est :
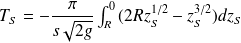
Soit :
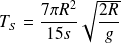
L'application numérique donne 11 minutes et 10 secondes.
Question
Clepsydre :
Soit un récipient (R0) à symétrie de révolution autour de l'axe Oz, de méridienne d'équation
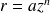
Où r est le rayon du réservoir aux points de cote z comptée à partir de l'orifice C, de faible section s = 1 cm2 percé au fond du réservoir.
Déterminer les coefficients constants n et a, donc la forme de (R0), pour que le cote du niveau d'eau placée dans (R0) baisse régulièrement de 6 cm par minute au cours de la vidange.
La clepsydre est caractérisée par une baisse du niveau par seconde constante :
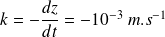
On peut encore écrire :
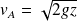et
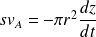
Soit :
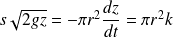
Or,
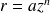, donc :
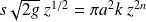
Cette relation est valable pour tout z, par conséquent n = 1 / 4. On en déduit également :
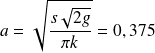
Finalement, l'équation de la méridienne est :
