Écoulement d'un fluide visqueux sur un plan incliné
(20 minutes de préparation)
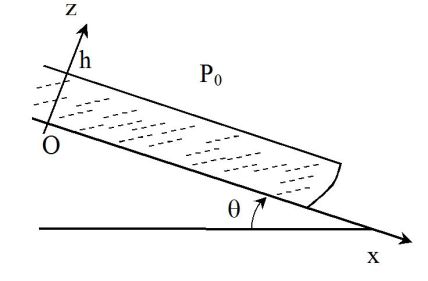
On considère l'écoulement permanent d'une couche de fluide incompressible et visqueux, de hauteur h, sur un plan incliné. On suppose l'écoulement unidimensionnel : le champ des vitesses sera parallèle à l'axe Ox et ne dépendra que de la variable z.
A la surface libre, la pression est uniforme et vaut P0.
La masse volumique du fluide, supposé newtonien, est ρ et sa viscosité
.
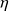On admettra qu'à cause de la faible viscosité de l'air au-dessus du fluide, il n'y a pas de contrainte tangentielle en z = h.
On donne l'équation de Navier-Stokes pour un fluide newtonien :
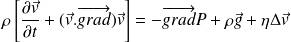
Question
Simplifier et projeter l'équation de Navier-Stokes.
En régime permanent :
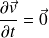
L'accélération convective vaut, avec les hypothèses de l'énoncé :
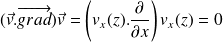
Par conséquent :
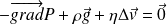
Question
Déterminer le champ des vitesses
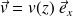en tenant compte des conditions aux limites.
L'équation précédente donne, en projection : (et P ne dépend pas de y)
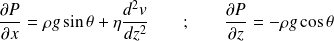
La deuxième équation donne par intégration :
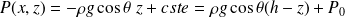
La 1ère devient alors, en remarquant que
:
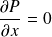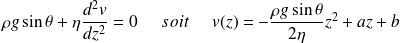
La vitesse est nulle en z = 0 et l'air n'exerce pas de force tangentielle sur le liquide en z = h, par conséquent
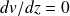en z = h. Ainsi :
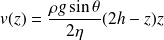
On obtient un profil de vitesses de type parabolique, avec un maximum en z = h.
Question
On s'intéresse à un écoulement de largeur L selon l'axe Oy, avec L >> h, pour pouvoir négliger les effets de bord. Calculer le débit volumique DV et en déduire la vitesse moyenne du fluide.
Le débit volumique vaut :
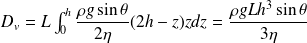
Et la vitesse moyenne de l'écoulement est :
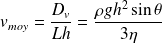
Question
On s'intéresse à une couche de glycérine pour laquelle :
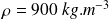et
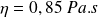
et d'épaisseur 1 mm. L'angle θ vaut 10°. Calculer la vitesse moyenne et commenter le résultat en utilisant le nombre de Reynolds.
On obtient :
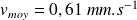
Et le nombre de Reynolds est :
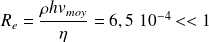
Les forces de viscosité sont bien suffisantes pour imposer un champ des vitesses laminaire.
