Exo 8
Question
Soient deux réels
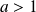et
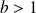. Calculer l'intégrale :
.
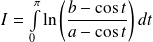Indice
Remarquez que l'intégrale peut s'écrire :
.
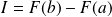Solution
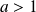et
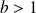, donc
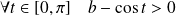et
.
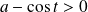Donc l'intégrale
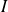est définie pour tout
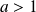et
.
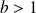Soit
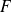la fonction définie par :
.
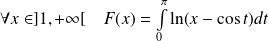Soit
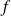la fonction définie par :
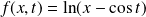sur
.
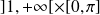Elle admet des dérivées partielles d'ordre
continues sur
:
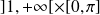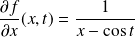et
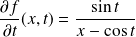
Donc la fonction
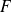est de classe
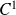sur
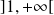et :
.
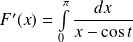On pose :
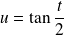, donc
et
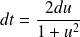. Donc :
.
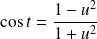Donc :
.
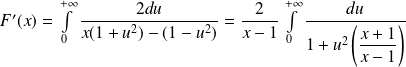On pose :
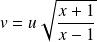, donc :
.
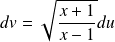Donc :
.
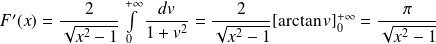Or :
.
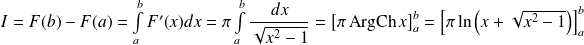Conclusion :
.
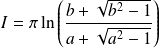