Exo 3
Question
Calculer la somme :
.
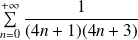Indice
Démontrez que la série est convergente, puis exprimez ses sommes partielles sous forme d'intégrales.
Solution
La série
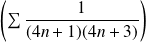est une série à termes positifs et :
.
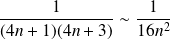Donc la série
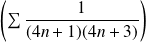est de même nature que la série
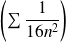, donc convergente.
La somme partielle d'ordre
est :
.
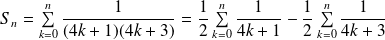Or :
.
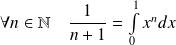Donc :
.
Donc :
.
Or :
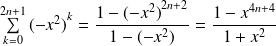pour tout
.
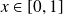Donc :
.
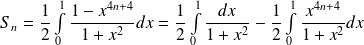Or :
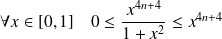. Donc :
.
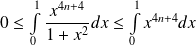Donc :
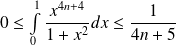. Donc :
.
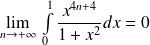Donc :
.
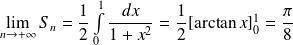Conclusion :
.
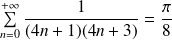