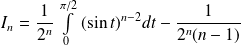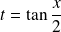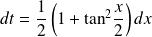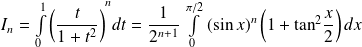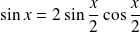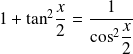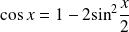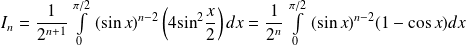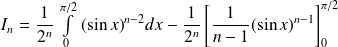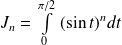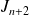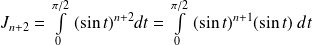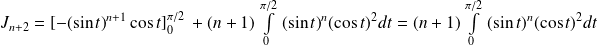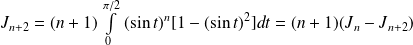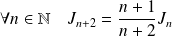Exo 2
Pour tout
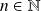 , on pose :
, on pose :
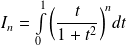 .
.
Question
Question
Question
Montrer que
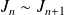 et en déduire un équivalent de
et en déduire un équivalent de
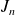 .
.
Indice
Etudiez le sens de variations de la suite
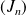 , puis introduisez la suite de terme général
, puis introduisez la suite de terme général
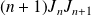 .
.
Solution
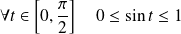 , donc
, donc
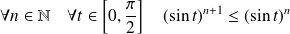 .
.
Donc :
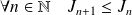 , donc :
, donc :
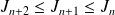 , donc :
, donc :
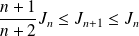 .
.
Or, sur
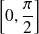 , la fonction
, la fonction
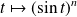 est continue, positive et non identiquement nulle.
est continue, positive et non identiquement nulle.
Donc :
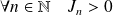 , et donc :
, et donc :
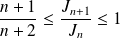 , donc :
, donc :
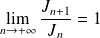 .
.
Conclusion :
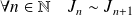 .
.
D'après 1) :
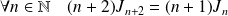 , donc
, donc
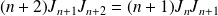 .
.
Donc la suite de terme général
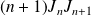 est constante, égale à
est constante, égale à
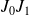 .
.
Or :
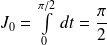 et :
et :
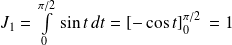 .
.
Donc :
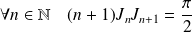 .
.
Or :
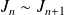 . Donc :
. Donc :
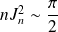 .
.
Conclusion :
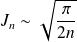 .
.
Question
En déduire un équivalent de
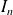 .
.
Solution
D'après la première question :
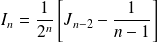 .
.
Or :
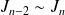 . Donc :
. Donc :
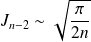 et
et
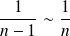 . Donc :
. Donc :
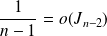 .
.
Conclusion :
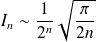 .
.