Exo 7
Question
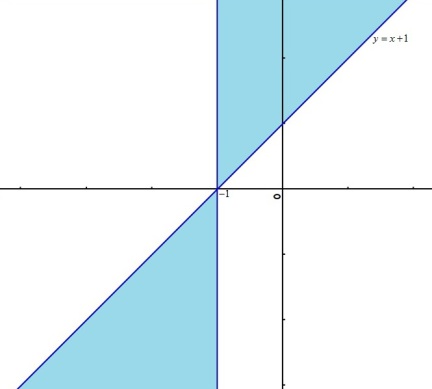
Déterminer dans
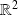 l'ensemble des points
l'ensemble des points
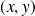 tels que l'intégrale
tels que l'intégrale
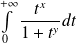 converge.
converge.
Comparez l'intégrale à des intégrales de Riemann.
Pour tout
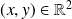 , la fonction
, la fonction
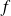 :
:
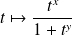 est continue sur
est continue sur
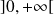 et positive.
et positive.
Donc l'intégrale
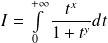 est impropre en
est impropre en
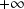 et dans certains cas en
et dans certains cas en
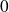 .
.
Donc on étudie la convergence des intégrales :
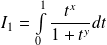 et
et
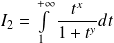 .
.
Si
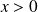 et
et
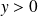 :
: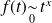 , donc l'intégrale
, donc l'intégrale
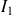 converge car
converge car
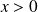 .
.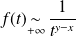 , donc l'intégrale
, donc l'intégrale
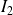 converge si et seulement si
converge si et seulement si
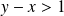 .
.
Donc, dans ce cas, l'intégrale
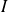 converge si et seulement si :
converge si et seulement si :
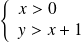 .
.
Si
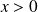 et
et
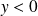 :
: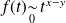 , donc l'intégrale
, donc l'intégrale
 converge car
converge car
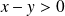 .
.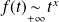 , donc l'intégrale
, donc l'intégrale
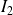 diverge.
diverge.
Donc, dans ce cas, l'intégrale
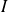 diverge.
diverge.
Si
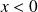 et
et
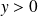 :
: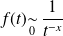 , donc l'intégrale
, donc l'intégrale
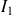 converge si et seulement si
converge si et seulement si
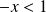 .
.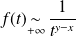 , donc l'intégrale
, donc l'intégrale
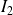 converge si et seulement si
converge si et seulement si
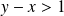 .
.
Donc, dans ce cas, l'intégrale
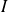 converge si et seulement si :
converge si et seulement si :
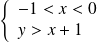 .
.
Si
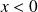 et
et
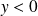 :
: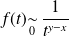 , donc l'intégrale
, donc l'intégrale
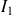 converge si et seulement si
converge si et seulement si
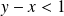 .
.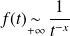 , donc l'intégrale
, donc l'intégrale
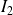 converge si et seulement si
converge si et seulement si
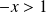 .
.
Donc, dans ce cas, l'intégrale
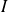 converge si et seulement si :
converge si et seulement si :
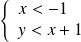 .
.
Si
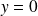 , alors :
, alors :
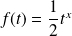 . Donc :
. Donc :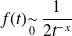 , donc l'intégrale
, donc l'intégrale
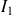 converge si et seulement si
converge si et seulement si
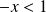 .
.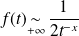 , donc l'intégrale
, donc l'intégrale
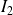 converge si et seulement si
converge si et seulement si
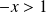 .
.
Donc, dans ce cas, l'intégrale
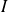 diverge car les conditions sont incompatibles.
diverge car les conditions sont incompatibles.
Si
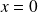 alors :
alors :
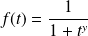 . Donc :
. Donc :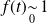 si
si
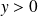 ,
,
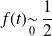 si
si
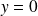 et
et
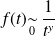 si
si
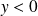 .
.Donc l'intégrale
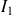 converge dans tous les cas.
converge dans tous les cas.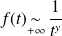 si
si
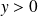 ,
,
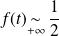 si
si
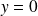 et
et
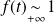 si
si
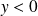 .
.Donc l'intégrale
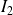 converge si et seulement si
converge si et seulement si
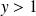 .
.
Donc, dans ce cas, l'intégrale
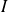 converge si et seulement si :
converge si et seulement si :
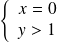 .
.
En résumé, l'intégrale
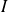 converge si et seulement si :
converge si et seulement si :
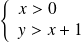 ou
ou
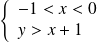 ou
ou
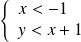 ou
ou
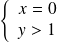 .
.
Conclusion : L'ensemble cherché est
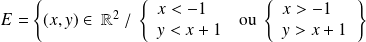 .
.
.