Exo 6
Les questions suivantes sont indépendantes.
Question
Etudier la convergence de la série réelle
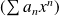où
.
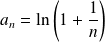Déterminez d'abord le rayon de convergence
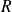de la série, puis étudiez la convergence aux bornes de l'intervalle
.
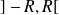Il s'agit d'une série entière. Soit
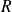son rayon de convergence.
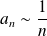. Donc :
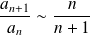. Donc :
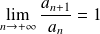. Donc :
.
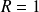Donc la série
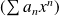converge absolument si
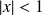, donc sur
.
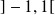Et si
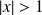, la série
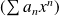diverge grossièrement.
Si
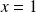, alors :
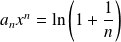, donc :
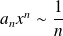. Donc la série
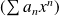est de même nature que la série harmonique
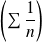, donc divergente.Si
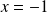, alors :
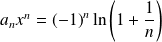. Donc la série
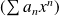est une série alternée dont le terme général décroit en valeur absolue vers
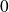.Donc la série
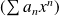est convergente (mais pas absolument convergente).
Conclusion : La série
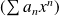est absolument convergente si
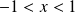, semi-convergente si
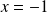, et divergente si
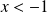ou si
.
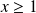Question
Etudier la convergence de la série réelle
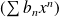où
.
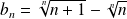Déterminez d'abord le rayon de convergence
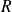de la série, puis étudiez la convergence aux bornes de l'intervalle
.
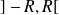Il s'agit d'une série entière. Soit
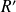son rayon de convergence.
.
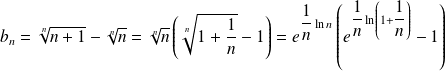Or :
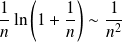, donc tend vers
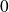. Donc :
.
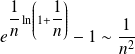Et :
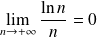, donc :
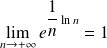. Donc :
.
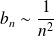Donc :
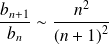. Donc :
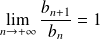. Donc :
.
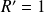Donc la série
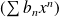converge absolument si
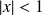, donc sur
.
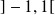Et si
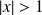, la série
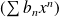diverge grossièrement.
Si
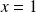, alors :
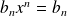, donc
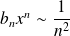. Donc la série
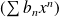est de même nature que la série de Riemann
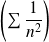, donc convergente.Si
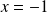, alors :
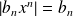, donc :
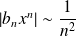.Donc la série
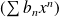est une série absolument convergente.
Conclusion : La série
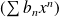est absolument convergente si
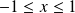, et diverge grossièrement si
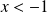ou
.
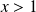