Exo 1
Soit un réel
.
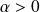Soit
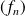la suite de fonctions définies par :
.
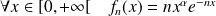Question
Etudier la convergence de la suite
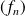suivant les valeurs de
.
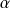Commencez par étudier la convergence simple.
Pour l'étude de la convergence uniforme, utilisez les variations des fonctions
.
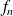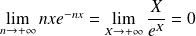, donc par croissances comparées :
.
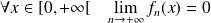Conclusion : Pour tout
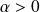, la suite
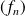converge simplement vers la fonction nulle.
Pour étudier la convergence uniforme, il faut étudier
.
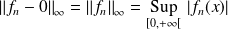Pour tout
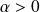, la fonction
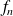est positive et dérivable sur
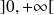, continue en
.
.
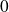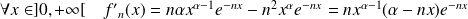On obtient le tableau de variations suivant :
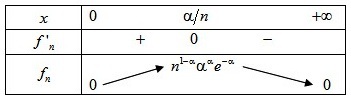
Donc le maximum est :
.
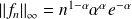La convergence est uniforme si et seulement si :
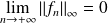, donc si :
.
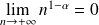Conclusion : La convergence est uniforme sur
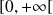si et seulement si
.
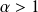