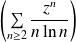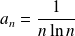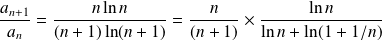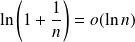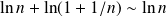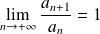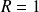Exo 5
Les questions suivantes sont indépendantes.
Question
Question
Déterminer le rayon de convergence de la série
.
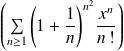Utilisez la règle de Cauchy.
Il s'agit d'une série entière
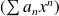avec
.
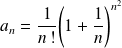Donc :
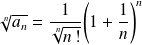. On sait que :
.
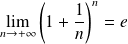Soit
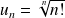. Donc :
.
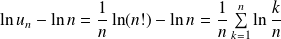C'est une somme de Riemann de la fonction :
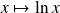intégrable et monotone sur
.
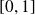Donc :
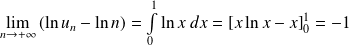. Donc :
.
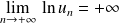Donc :
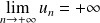. Donc :
.
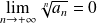Conclusion : Le rayon de convergence de la série
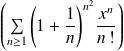est
.
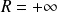Question
Déterminer le rayon de convergence de la série de terme général
.
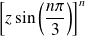Calculez
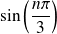suivant les valeurs de
.
Il s'agit d'une série entière
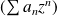avec
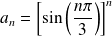. Soit
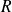son rayon de convergence.
Or :
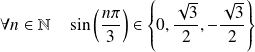, donc :
.
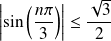Donc la série à termes positifs
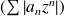est majorée par la série géométrique
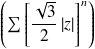qui converge si :
.
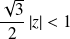Donc la série
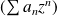est absolument convergente si :
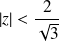. Donc :
.
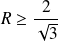Or, si
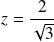, alors :
.
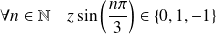Donc la série
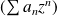diverge car son terme général ne tend pas vers
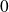. Donc :
.
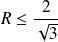Conclusion : Le rayon de convergence de la série de terme général
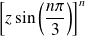est
.
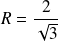