Exo 2
Soit
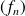la suite de fonctions définies par :
.
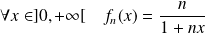Question
Montrer que la suite
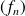converge simplement, mais pas uniformément sur
.
Commencez par étudier la convergence simple.
Pour l'étude de la convergence uniforme, utilisez une suite.
Pour tout
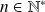, si
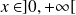, alors :
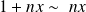, donc :
.
Conclusion : La suite
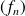converge simplement sur
vers la fonction
:
.
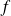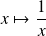Or :
.
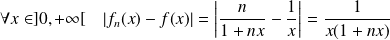Donc pour la suite de terme général
, on a :
.
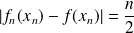Donc il existe une suite
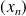de
telle que :
.
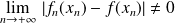Conclusion : La convergence n'est pas uniforme sur
.
Par contre, la fonction définie par :
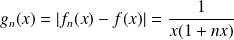est décroissante.
Donc, si
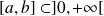, alors :
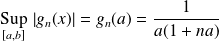, et donc :
.
Donc la convergence est uniforme sur tout segment contenu dans
.
Conclusion : Sur
, il y a convergence uniforme locale.
