Variables aléatoires à densité
On considère un espace probabilisé
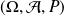 dont l'univers
dont l'univers
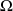 n'est pas dénombrable.
n'est pas dénombrable.
Définition :
Une variable aléatoire
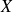 est absolument continue si sa fonction de répartition
est absolument continue si sa fonction de répartition
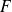 est continue sur
est continue sur
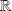 et de classe
et de classe
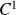 sur
sur
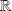 sauf peut-être en un nombre fini de points.
sauf peut-être en un nombre fini de points.
Toute fonction
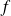 vérifiant
vérifiant
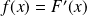 en tout point où
en tout point où
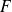 est dérivable est appelée densité de probabilité de
est dérivable est appelée densité de probabilité de
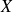 .
.
Une telle variable aléatoire est aussi appelée variable à densité.
L'ensemble
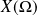 des valeurs prises par
des valeurs prises par
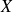 est l'ensemble des réels
est l'ensemble des réels
 pour lesquels
pour lesquels
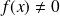 .
.
Attention :
On peut remarquer qu'il peut exister plusieurs densités de probabilité. Elles coïncident aux points où
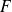 est dérivable, mais pas ailleurs.
est dérivable, mais pas ailleurs.
Définition :
Une fonction
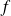 définie sur
définie sur
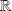 est une densité de probabilité si :
est une densité de probabilité si :
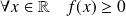 .
.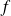 est continue sur
est continue sur
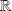 sauf peut-être en un nombre fini de points.
sauf peut-être en un nombre fini de points.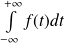 est convergente et
est convergente et
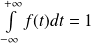 .
.
On admettra qu'il existe alors un espace probabilisé et une variable aléatoire
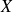 dont la fonction
dont la fonction
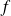 est une densité de probabilité.
est une densité de probabilité.
Exemple :
Soit
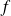 la fonction définie par :
la fonction définie par :
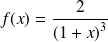 si
si
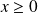 et
et
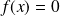 sinon.
sinon.
Montrer que la fonction
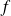 est une densité de probabilité.
est une densité de probabilité.
Fondamental :
Propriétés
Si
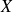 est une variable aléatoire de densité
est une variable aléatoire de densité
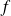 , alors :
, alors :
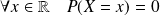 .
.Sa fonction de répartition est :
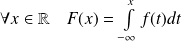 .
.Sa fonction de répartition est croissante sur
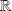 .
. Elle vérifie :
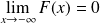 et
et
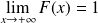 .
.Sa fonction de répartition est continue sur
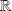 et de classe
et de classe
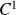 sauf peut-être en un nombre fini de points. Là où elle est dérivable :
sauf peut-être en un nombre fini de points. Là où elle est dérivable :
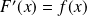 .
.
On reprend l'exemple précédent.
Exemple :
La fonction de répartition
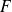 est définie par :
est définie par :
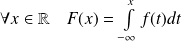 .
.
Cette intégrale est convergente pour tout réel
 puisque
puisque
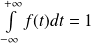 .
.
Donc :
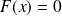 si
si
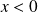 et
et
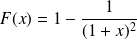 si
si
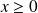 .
.
Comme pour les variables aléatoires discrètes, on peut exprimer les probabilités des événements liés à
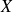 à l'aide de la fonction de répartition.
à l'aide de la fonction de répartition.
Mais, comme
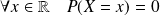 , les résultats sont les mêmes que les inégalités soient larges ou strictes.
, les résultats sont les mêmes que les inégalités soient larges ou strictes.
Par exemple :
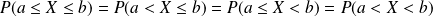 .
.
Fondamental :
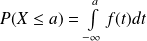 .
.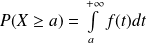 .
.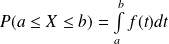 .
.
Les opérations sur les variables aléatoires à densité sont les mêmes que pour les variables discrètes :
Somme
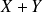 de deux variables aléatoires.
de deux variables aléatoires.Produit
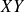 de deux variables aléatoires.
de deux variables aléatoires.Image
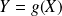 d'une variable aléatoire
d'une variable aléatoire
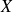 par une fonction
par une fonction
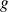 .
.





